ГАЛУА ТЕОРИЯ КОЛЕЦ

ГАЛУА ТЕОРИЯ КОЛЕЦ - обобщение результатов теории Галуа полей на случай ассоциативных колец с единицей. Пусть А - ассоциативное кольцо с единицей, Н - некоторая подгруппа группы всех автоморфизмов кольца А, N - подгруппа группы Н,

J(N) = {a ∈ A | h(a) = a ∀h ∈ N},

B = J(H). Тогда J(N)- подкольцо кольца А. Пусть В₁ - подкольцо кольца А. Говорят, что автоморфизм h кольца А составляет кольцо В₁ поэлементно инвариантным, если h(b) = b для всех b ∈ В₁. Множество всех таких автоморфизмов обозначается G(B₁). Пусть

H(B₁) = G(B₁) ∩ H и В₁ ⊇ В. Основной объект изучения Г. к. т.- соответствия: 1) N → J(N); 2) В₁ → G(В₁); 3) В₁ → Н(B₁).

В отличие от теории Галуа полей (даже в том случае, когда группа Н конечна) здесь не всегда выполняется равенство G(B₁) = H(В₁), а соответствия 1), 2) и 1), 3) не обязаны быть взаимно обратными. Поэтому представляет интерес выделение таких семейств подколец и семейств подгрупп, для к-рых справедлив аналог теоремы о соответствиях Галуа. В двух случаях эта задача получила удовлетворительное решение. Первый из них характеризуется требованием «близости» свойств кольца А к свойствам поля (напр., А - тело или полное кольцо линейных преобразований векторного пространства над телом), второй - требованием «близости» строения кольца А над подкольцом В к строению соответствующей пары в случае, когда А -поле (напр., В-модуль проективен).

Пусть с - обратимый элемент кольца А и Т_c : А → А -автоморфизм кольца А, определяемый равенством Т_c(х) = схс^-1, х ∈ А, R(H) - подалгебра алгебры А, порожденная обратимыми элементами с ∈ А, для которых Т_c ∈ Н. Группа Н наз. N-группой, если Т_x ∈ Н для всех обратимых x ∈ R(H). Если А - тело, В - его подтело, причем B = J(G(B)), А - конечномерное левое векторное пространство над В, то соответствия Галуа H → J(Н) и D → G(D) являются обратными друг к другу, где H принадлежит множеству всех N-подгрупп группы G(B), a D- множеству всех подтел тела А, содержащих тело В.

Аналогичный результат справедлив и в том случае, когда А - полное кольцо линейных преобразований (однако соответствующая система условий, выделяющая семейства подгрупп и семейства подколец, формулируется несколько сложнее).

Пусть далее А - коммутативное кольцо без нетривиальных идемпотентов и А ⊇ В. Кольцо А наз. конечным нормальным расширением кольца В, если В = J(G(B)) и А - конечно порожденный B-модуль. Кольцо А можно рассматривать как А ⊗_B А -модуль, полагая

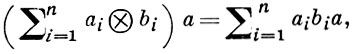
где а_i, b_i, а ∈ А. Кольцо А наз. сепарабельной В-алгеброй, если А - проективный А ⊗_B А - модуль. Если А - конечное нормальное сепарабельное расширение кольца В, то А - конечно порожденный проективный B-модуль, группа G(B) конечна ([G(B) : 1] = rank_B А) и отображения Н → J(H), B₁ → G(B₁) задают взаимно обратные соответствия между множеством всех подгрупп группы G(B) и множеством всех сепарабельных B-подалгебр алгебры А.

Всякое кольцо В обладает сепарабельный замыканием, являющимся аналогом сепарабельного замыкания поля. Группа всех автоморфизмов этого замыкания, оставляющих кольцо В поэлементно инвариантным, оказывается, в общем случае, проконечной группой. Соответствия 1) и 2) являются взаимно обратными на множестве всех замкнутых подгрупп полученной группы и на множестве всех сепарабельных B-подалгебр сепарабельного замыкания кольца В.

Аналогичные результаты справедливы и в том случае, когда кольцо В содержит нетривиальные идемпотенты. При этом, однако, ряд основных понятий подвергается существенному изменению. Напр., роль группы Галуа G(B) играет фундаментальный группоид.

Лит.: [1] Джекобсон Н., Строение колец, пер. с англ., М., 1961; [2] Сhasе S. U., Swedler М. Е., Hopf algebras and Galois theory, В.-Hdlb.-N. Y., 1969; [3] De Meyer F., Ingraham E., Separable algebras over commutative rings, В.-Hdlb.-N. Y., 1971; [4] Magid A. R., The separable Galois theory of commutative rings, N. Y., 1974.

К. И. Бейдар, А. В. Михалев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.