
ГАЛУА ПОЛЕ
ГАЛУА ПОЛЕ, конечное поле, - поле, число элементов к-рого конечно. Г. п. впервые рассматривалось Э. Галуа (Е. Galois, см. [1], с. 35 - 47).
Число элементов любого Г. п. есть степень рn нек-рого натурального простого числа р, являющегося характеристикой этого поля. Для любого натурального простого р и любого натурального n существует (и единственно, с точностью до изоморфизма) поле из рn элементов. Оно обозначается GF(pn) или Fpn. Поле GF(pm) содержит в качестве подполя поле GF(pn) в том и только в том случае, когда m делится на n. В частности, в любом поле GF(pn) содержится поле GF (р), наз. простым полем характеристики р. Поле GF(p) изоморфно полю Z/(р) классов вычетов кольца целых чисел по простому модулю р. В любом фиксированном алгебраическом замыкании Q поля GF(p) существует точно одно подполе GF (рn) для каждого n. Соответствие n ↔ GF(pn) является изоморфизмом между решеткой натуральных чисел относительно делимости и решеткой конечных алгебраич. расширений поля GF(p), лежащих в Ω, относительно включения. Такова же решетка множества конечных алгебраич. расширений любого Г. п., лежащих в его фиксированном алгебраич. замыкании.
Алгебраич. расширение GF(pn)/GF(p) является простым, т. е. существует примитивный элемент α ∈ GF(pn) такой, что GF (pn) = GF (р)(α). Таким α будет любой корень каждого неприводимого многочлена степени n из кольца GF(p)[X]. Число примитивных элементов расширения GF(pn)/GF(р) равно
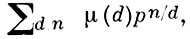
где μ - Мёбиуса функция. Аддитивная группа поля GF(pn) естественным образом наделяется структурой n-мерного векторного пространства над GF(p). В качестве базиса можно взять 1, α, ..., αn-1. Ненулевые элементы поля GF(pn) образуют мультипликативную группу GF*(pn) порядка рn - 1, т. е. каждый элемент из GF* (рn) является корнем многочлена Хpn-1 - 1. Группа GF*(рn) циклическая, ее образующие - первообразные корни из единицы степени рn - 1, число к-рых равно φ(рn - 1), где φ - Эйлера функция. Каждый первообразный корень из единицы степени рn - 1 является примитивным элементом расширения GF(pn)/GF(р), но не наоборот. Точнее, среди
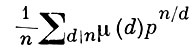
неприводимых унитарных многочленов степени n над GF(p) имеется 1/n φ(рn - 1) таких, корни к-рых будут образующими для GF*(рn).
Множество элементов поля GF(pn) в точности совпадает с множеством корней многочлена Хpn - Х в Ω, т. е. GF(pn) характеризуется как подполе элементов из Ω, инвариантных относительно автоморфизма τ : х → хpn, наз. автоморфизмом Фробениуса. Если GF(pm) ⊃ GF(pn), то расширение GF(pm)/GF(рn) нормально (см. Расширение поля), его Галуа группа Gal(GF(рm)/GF(рn)) циклическая порядка min. В качестве образующей группы Gal (GF (pm)/GF (рn)) может быть взят автоморфизм τ.
Лит.: [1] Галуа Э., Сочинения, пер. с франц., М.-Л., 1936; [2] Ван дер Варден Б. Л., Алгебра, пер. с нем., М., 1976, с. 158 - 62; [3] Чеботарев Н. Г., Основы теории Галуа, М.-Л., 1934, ч. 1, с. 154-62; [4] Бурбаки Н., Алгебра. Многочлены и поля. Упорядоченные группы, пер. с франц., М., 1965, с. 185-203.
А. И. Скопин.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'