ГАЛЕРКИНА МЕТОД

ГАЛЕРКИНА МЕТОД, метод моментов, - метод нахождения приближенного решения операторного уравнения в виде линейной комбинации элементов заданной линейно независимой системы.

Пусть F(х) - нелинейный оператор, область определения к-рого лежит в банаховом пространстве X, а область значений - в банаховом пространстве Y. Для решения уравнения

F(x) = h (1)

методом Галеркина выбираются линейно независимая система элементов из X (координатная система) {φ_i}^∞₁ и линейно независимая система функционалов {ψ_j}^∞₁ из пространства Y*, сопряженного к Y (проекционная система). Приближенное решение х уравнения (1) разыскивается в виде

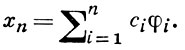
(2)

Числовые коэффициенты c₁, ..., c_n определяются из системы уравнений

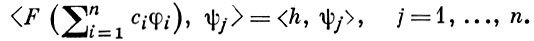
(3)

В этой общей постановке задачи нельзя гарантировать, что система (3) имеет хотя бы одно решение. В случае если (3) имеет единственное решение при каждом n = 1, 2, ..., приближенное решение (2) может не сходиться при n → ∞ даже слабо к точному решению уравнения (1). Тем не менее, Г. м. является мощным средством не только для нахождения приближенных решений, но и для доказательства теорем существования решений линейных и нелинейных уравнений, особенно в задачах для уравнений с частными производными.

В ряде случаев задача определения коэффициентов (2) из системы (3) эквивалентна задаче об отыскании минимума нек-рого функционала, и Г. м. превращается в вариационный (энергетический) метод. Наиболее важный из таких методов - Ритца метод. В нек-рых случаях эффективно применение для исследования системы (3) топологич. методов.

Если пространства X и Y гильбертовы, то Г. м. иногда наз. методом Галеркина-Петрова. Если, кроме того, координатная и проекционная системы совпадают: X = Y = H и ψ_i = φ_i, то принято говорить о методе Бубнова-Галеркина. Если X = Y = H - гильбертово пространство, а ψ_i = F(φ_i), то этот частный случай Г. м. наз. наименьших квадратов методом.

В линейном случае, когда F(x) ≡ Aх, A - линейный, вообще говоря, неограниченный оператор с областью определения D(A) ⊆ X и с областью значений R(A) ⊆ Y, а координатная система выбрана в D(А), уравнение (1) принимает вид:

Ax = h. (4)

При этом система (3) представляет собой систему n линейных уравнений с n неизвестными:

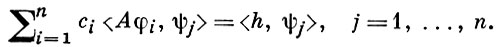
(5)

Если в условиях метода наименьших квадратов на R(А) существует и ограничен обратный оператор А^-1, h ∈ R(A) и система {Aφ_i}^∞₁ полна в H, то приближенное решение (2) при n → ∞ сходится к точному решению уравнения (4). Если в условиях метода Галеркина-Петрова оператор A симметричен, положительно определен, h ∈ R(A) и система {φ_i}^∞₁ полна в гильбертовом пространстве Н_A - пополнении D(A) в метрике, порожденной скалярным произведением

[x, y] = (Ax, у), х, y ∈ D(A),

то приближенное решение (2) сходится к точному решению уравнения (4) как в Н_A, так и в H.

Если A - самосопряженный положительно определенный оператор в H, а {φ_i}^∞₁ - полная ортонормированная система его собственных элементов, то метод Бубнова-Галеркина и метод наименьших квадратов совпадают с Фурье методом.

Г. м. применяется также для приближенного решения задач на собственные значения и собственные элементы.

Г. м. получил широкое распространение после исследований Б. Г. Галеркина [1]; ранее он применялся для решения конкретных задач теории упругости И. Г. Бубновым. Существует общий подход к приближенным методам, охватывающий обобщающие Г. м. проекционные методы, разностные методы и другие приближенные методы.

Лит.: [1] Галеркин Б. Г., «Вестник инженеров», 1915, т. 1, № 19, с. 897-908; [2] Михлин С. Г., Вариационные методы в математической физике, М., 1957; [3] Вайнберг М. М., Вариационный метод и метод монотонных операторов в теории нелинейных уравнений, М., 1972.

В. А. Треногин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.