ГАЗОВЫХ СТРУЙ ТЕОРИЯ

ГАЗОВЫХ СТРУЙ ТЕОРИЯ - раздел газовой динамики, в к-ром исследуются течения газа в предположении, что газ частично обтекает встречаемое на пути своего распространения препятствие и стекает с него, образуя за препятствием застойную область. Решение задач о струйном течении газа достигается в предположении, что газ баротропный и движение его плоскопараллельное, потенциальное и установившееся. В этих предположениях выводится из уравнений гидродинамики следующая основная формула:

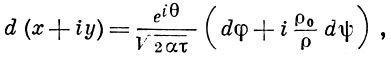
(1)

в к-рой φ и ψ - соответственно потенциал скоростей и функция тока, ρ - плотность газа в произвольной точке, ρ₀ - плотность газа в точке нулевой скорости газа. Для адиабатич. движений постоянная α есть квадрат скорости звука в точке нулевой скорости газа, поделенный на γ-1 (γ - показатель адиабаты). Для решения задач Г. с. т. целесообразно рассматривать искомые функции не в зависимости от переменных х, у -координат в плоскости потока, а как функции переменных Чаплыгина: τ = |v|²/2α и угла θ наклона вектора скорости v к оси Ох. При таком выборе независимых переменных уравнение (1) приводит к системе двух уравнений с частными производными

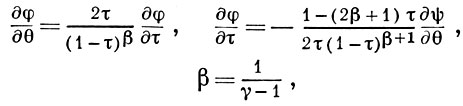
к к-рой надо присоединить интеграл Бернулли

ρ = ρ₀(1 - τ)^β.

Исключение функции φ(θ, τ) приводит к уравнению для функции тока:

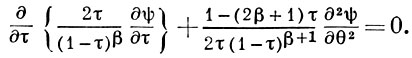
(2)

Это - уравнение эллиптич. типа для дозвуковых течений и гиперболич. типа для сверхзвуковых течений. Решение уравнения (2) может быть получено для ряда препятствий, составленных из отрезков прямых линий; вдоль каждого такого отрезка переменное θ имеет соответствующее постоянное значение. Вдоль линий тока, срывающихся с концов отрезков и являющихся границей, отделяющей движущийся газ от спокойного газа в застойной области, переменное τ имеет постоянное значение. Функция тока ψ(θ, τ) = const в точках границ θ = const и τ = const. На плоскости переменных θ, τ образуется область, ограниченная отрезками прямых линий, параллельных осям координат; вдоль каждого такого отрезка функция тока имеет постоянное значение. Расположение этих отрезков и постоянные значения функции ψ(θ, τ) на них зависят от вида и положения препятствия на плоскости течения газа. В определенном круге задач функция ψ(θ, τ) может быть получена из уравнения (2) методом разделения переменных. Напр., если поток газа дебита Q и конечной ширины набегает на прямолинейную пластинку, поставленную перпендикулярно к скорости газа в удаленных частях потока, то функция ψ(θ, τ) определяется рядом:

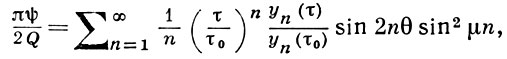
(3)

где τ₀ - значение переменной τ на граничной линии тока, μ - угол скорости потока с осью Ох далеко за пластинкой. Угол μ может быть найден через длину, а сила давления потока на пластинку - с помощью формулы (1).

Функция у_n(х) получается при разделении переменных в уравнении (2) и является интегралом гипергеометрич. уравнения:

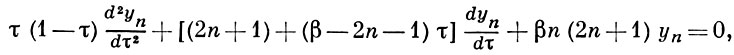
голоморфным около точки τ = 0.

Функция ψ(θ, τ) для газа, вытекающего из отверстия бесконечно широкого сосуда, определяется рядом

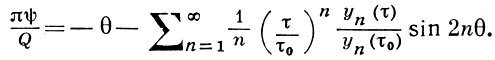
(4)

Сходимость рядов вида (3) и (4) была установлена С. А. Чаплыгиным (см. [1]) для дозвуковых течений, т. е. при τ < 1/(2β+1).

Ряды, подобные рядам (3) и (4) для функции ψ(θ, τ), могут быть составлены, если в потоке есть лишь одна характерная для него скорость, отличная от нуля. Если же имеются две или несколько характерных скоростей, как, напр., в задаче о вытекании газа из отверстия в поперечной стенке сосуда, ограниченного двумя бесконечными полупрямыми, то решение выражается с помощью определенных интегралов сложной структуры, содержащих θ и τ в виде параметров.

Для исследования рядов вида (3), (4) и определенных интегралов, дающих точное решение задач Г. с. т., С. А. Чаплыгин предложил приближенный метод решения задач о струйном движении газа. Этот метод приводит задачу о движении газа к задаче о плоскопараллельном потенциальном движении несжимаемой жидкости.

Лит.: [1] Чаплыгин С. А., Собр. соч., т. 2, М.-Л., 1948, с. 19-137; [2] Бай Ши-и, Теория струй, пер. с англ , М., 1960.

Л. Н. Сретежкий.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.