ВЫЧЕТ-ФОРМА

ВЫЧЕТ-ФОРМА, форма-вычет,- обобщение понятия вычета аналитич. функции одного комплексного переменного на случай многих переменных. Пусть X - комплексное аналитич. многообразие, S - его аналитич. подмногообразие комплексной коразмерности 1 и пусть ω(х) - замкнутая внешняя дифференциальная форма класса С^∞ на X\S, имеющая на S полярную особенность 1-го порядка. Последнее означает, что для функции s(x, у), голоморфной от x в окрестности U_y точки у ∈ S и такой, что

S ∩ U_y = {x: s(х, y) = 0}, ds ≢ 0 при х = у,

форма ω(х) ⋅ s(x, y) принадлежит классу C^∞(U_y). При этих условиях в окрестности U любой точки у ∈ S существуют такие формы ψ(х, у), θ(х, у) класса С^∞, что

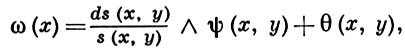
причем ψ(х, y)|_S∩Uy есть замкнутая форма класса С^∞, зависящая только от ω. Замкнутая форма на S, определяемая в окрестности каждой точки у ∈ S, сужением ψ(x, y)|_S∩Uy , наз. вычет-формой формы ω и обозначается

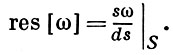
Если форма ω голоморфна, то и ее В.-ф. голоморфна. Напр., для X = ℂⁿ, S = {х ∈ ℂⁿ: s(x) = 0} и формы

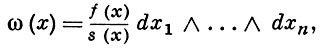
где f, s- голоморфные функции в ℂⁿ, grad s ≠ 0 на S, В.-ф. равна

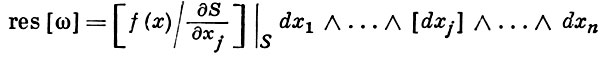
в точках, где dS/dx_j ≠ 0.

Для В.-ф. имеет место формула вычета:

∫_δγ ω = 2πi ∫_γ res[ω],

где γ - произвольный цикл в S размерности, равной степени res [ω], δγ - цикл в X\S -граница нек-рой цепи в X, находящейся в общем положении с S и пересекающейся с S по γ.

Кратная В.-ф. res^m[ω] определяется по индукции. Вычет-класс (или класс-вычет) замкнутой в X\S формы ω есть класс когомологий подмногообразия S, образованный В.-ф. форм класса С^∞ в X\S, когомологичных со и имеющих на S полярную особенность 1-го порядка. Вычет-класс формы со обозначается Res [ω]. Вычет-класс голоморфной формы может не содержать голоморфной формы, так что в общем случае нельзя ограничиться рассмотрением кольца голоморфных форм вместо кольца замкнутых форм. Однако это возможно, если X - Штейна многообразие. Вычет-класс Res[ω] не зависит от выбора ω из одного и того же класса когомологий и осуществляет гомоморфизм группы классов когомологий многообразия X\S в группу классов когомологий многообразия S:

Res: H*(X\S) → Н*(S).

Как и для В.-ф., справедлива формула вычета:

∫_δγ ω = 2πi ∫_γ Res[ω],

причем интеграл в правой части берется от любой формы из вычет-класса Res [ω] и не зависит от ее выбора. Лит. см. при ст. Вычет аналитической функции [7], [8], [4].

А. П. Южаков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.