ВЫСОТА

ВЫСОТА в диофантовой геометрии - некоторая численная функция на множестве решений диофантова уравнения. В простейшем случае целочисленного решения (x₁, ..., x_n) диофантова уравнения высота есть функция решения, равная max |x_i|. В таком виде она встречается уже в методе спуска Ферма. Пусть имеется проективное алгебраич. многообразие X, определенное над глобальным полем K. Высота представляет собой класс действительнозначных функций h_L(P), определенных на множестве X(K) рациональных точек Р, и зависящий от морфизма L: Х → Рⁿ многообразия X в проективное пространство Рⁿ. Каждая функция из этого класса тоже наз. высотой. Различие между функциями из этого класса с точки зрения оценки рациональных точек несущественно; для любых двух функций h'_L и h''_L существуют такие константы с' > 0 и с'' > 0, что c'h'_L ≤ h''_L ≤ c''h'_L. Такие функции наз. эквивалентными; эта эквивалентность (здесь) обозначается .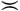

Основные свойства В. Функция h_L(P) функториальна по Р, т. е. для любого морфизма f: X → Y и морфизма L : Y → Pⁿ

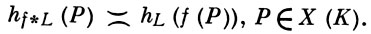
Если морфизмы L, L₁ и L₂ определяются обратимыми пучками ℒ, ℒ₁ и ℒ₂ и ℒ = ℒ₁ ⊗ ℒ₂, то h_L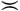 h_L1h_L2. Множество точек Р ∈ X(K), имеющих ограниченную В., конечно в следующем смысле: если основное поле К есть поле алгебраич. чисел, то указанное множество конечно; если же K - поле алгебраич. функций с полем констант k, то элементы X(K) зависят от конечного числа параметров из поля k и, в частности, К конечно, если поле k конечно. Пусть |⋅|_V пробегает множество всех нормирований поля К. Тогда В. точки (х₀:х₁: ... :х_n) проективного пространства Рⁿ с координатами из К может быть определена как

(*)

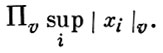
Корректность определения следует из формулы произведения П_v|x|_v = 1, x ∈ К. Пусть X - произвольное проективное многообразие над К и L - замкнутое вложение многообразия X в проективное пространство, В. h_L можно получить, перенося функцию (*) с помощью этого вложения на множество X(K). Различные проективные вложения, соответствующие одному и тому же пучку ℒ, определяют на X(K) эквивалентные функции. Распространение по линейности дает требуемую функцию h_L. Иногда вместо функции h_L используют ее логарифм - так наз. логарифмич. высоту.

Приведенные выше оценки являются в нек-рых случаях следствием точных равенств (см. [3], [4], [5]). Существует вариант функции В.- высота Тейта-Нерона, к-рая определяется на абелевых многообразиях и ведет себя функториальным образом относительно морфизмов абелевых многообразий, сохраняющих нулевую точку. Локальный аспект развит в [6]. Построенные там локальные компоненты В. играют в арифметике роль индексов пересечения.

Лит.: [1] Вейль А., Теория чисел и алгебраическая геометрия, «Математика», 1958, т. 2, № 4; [2] Lang S., Diophantine geometry, N. Y.-L., 1962; [3] Манин Ю. П., Теорема Морделла-Вейля, в кн.: Мамфорд Д., Абелевы многообразия, пер. с англ., М., 1971, с. 279-95; [4] Манин Ю. И., «Изв. АН СССР. Сер. матем.», 1964, т. 28, с. 1363-90; [5] Мumfоrd D., «Аmеr. J. Math.», 1965, v. 87, р. 1007-16; [6] Néron А., «Аnn. Math.», 1965, v. 82, p. 249-331.

A. H. Паршин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.