ВЫРОЖДЕННОЕ УРАВНЕНИЕ

ВЫРОЖДЕННОЕ УРАВНЕНИЕ с частными производными - дифференциальное уравнение с частными производными, тип к-рого вырождается в нек-рых точках области задания уравнения или на ее границе. Тип уравнения или системы уравнений в точке определяется одним или несколькими алгебраич. соотношениями между коэффициентами. Среди этих соотношений имеются, как правило, строгие неравенства. Если в нек-рых точках рассматриваемой области вместо строгих неравенств выполняются нестрогие, то говорят о вырождении типа, а уравнение (система уравнений) наз. вырождающимся, или вырожденным. Различают вырожденные эллиптические уравнения, вырожденные гиперболические уравнения, вырожденные параболические уравнения (системы уравнений).

Примеры:

хu_x⁴ + u_y⁴ + u_z⁴ + u_x = 0

- вырожденное эллиптич. уравнение в полупространстве х ≥ 0;

y²u_yy - u_xx = 0

- вырожденное гиперболич. уравнение во всей плоскости;

-u_t + u_yy + уu_x = 0

- вырожденное параболич. уравнение в области t ≥ 0;

yu_x - v_y = 0, u_y + v_x = 0

- вырожденная эллиптич. система при у ≥ 0.

В. у. встречаются в теории пограничного слоя, в безмоментной теории оболочек, в теории диффузионных процессов, в частности в теории броуновского движения, и во многих других задачах механики и физики.

Исследования В. у. ведутся по двум тесно связанным между собой направлениям: 1) доказывается разрешимость краевых задач с учетом тех изменений в постановке, к-рые происходят в силу вырождения типа; 2) устанавливаются свойства решений, аналогичные свойствам невырожденных уравнений (гладкость, неравенства Гарнака для эллиптич. и параболич. уравнений и т. п.).

Наиболее полно изучены В. у. 2-го порядка эллиптич. и параболич. типов (строго говоря, параболич. уравнение тоже можно считать вырожденным эллиптич. уравнением, удовлетворяющим дополнительным условиям). В случае, когда вырождение типа имеется не только на границе, но и во внутренних точках (напр., во всех точках рассматриваемой области), такие уравнения называют еще уравнениями с неотрицательной характеристической формой, эллиптикопараболическими уравнениями, ультрапараболическими уравнениями.

Особенностью В. у. является специфич. постановка краевых задач. Граничные условия иногда приходится задавать не на всей границе, а на ее части. М. В. Келдыш впервые обратил внимание на зависимость постановки краевой задачи от характера вырождения эллиптич. уравнения на границе. Для общего эллиптикопараболич. уравнения 2-го порядка

a^ik(х) u_xixk + b^l(х)u_xi + c(x)u = f(х); a^ikξ_iξ_k ≥ 0, (*)

первая краевая задача ставится следующим образом. Пусть Г - граница рассматриваемой области D, n = (n₁, ..., n_m) - внутренняя нормаль к Г, а Г̃ - та часть Г, где а^ikn_in_k = 0 и (bⁱ - а^ij_xj)n_i ≥ 0. Требуется найти решение уравнения (*) в области D так, чтобы u|_Г\Г̃ = φ. Выли доказаны существование и единственность обобщенного решения этой задачи и указаны достаточные условия, при к-рых обобщенное решение будет гладким.

Так как частным случаем В. у. являются уравнения 1-го порядка, то ясно, что решения вырожденных эллиптич. уравнений, вообще говоря, не будут гладкими внутри области, если граничные условия недостаточно гладкие. Однако примеры показывают, что и при бесконечно дифференцируемых граничных условиях и коэффициентах В. у. его решения могут не быть бесконечно дифференцируемыми. Найдено условие гипоэллиптичности для общего вырожденного эллиптич. уравнения 2-го порядка.

Свойства решений вырожденных эллиптич. и параболич. уравнений 2-го порядка изучаются как с помощью геометрич. методов, так и с помощью методов теории вероятностей.

Большинство исследований вырожденных гиперболич. уравнений относится к уравнениям 2-го порядка с двумя независимыми переменными, вырождающимся на границе области. Эти работы стимулировались прежде всего изучением уравнений смешанного типа и связанных с ними задач газовой динамики. Для иллюстрации возникающих здесь вопросов рассмотрим задачу Коши (u(х, 0) = α(х), u_y(х, 0) = β(х)) для уравнения с главной частью u_yy - у^mu_xx. При m < 2 эта задача имеет единственное решение, а при m > 2 задача Коши, вообще говоря, некорректна. Для уравнения с главной частью y^mu_yy - u_xx задача Коши с данными на линии вырождения поставлена корректно при 0 < m < 1. Если m ≥ 1, то так же, как и для эллиптич. уравнения, постановка задачи, вообще говоря, видоизменяется. Вместо u_y(х, 0) задается lim_y→0 ρ(y) u_y(x, y), где ρ(у) - нек-рая положительная функция, зависящая от коэффициентов уравнения.

Для гиперболич. уравнения с большим числом пространственных переменных

u_tt - (a^ij(t, х) u_xi)_xj + bⁱ(t, х)u_xi + b(t, х) u_t + c(t, x)u = f,

вырождающегося как на начальной плоскости t = 0, так и внутри области, доказана корректность задачи Коши при выполнении нек-рых условий. Наиболее существенным из этих условий является выполнение неравенства

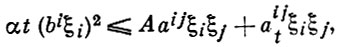
где α и А - нек-рые положительные постоянные.

Ряд результатов для линейных В. у. переносится и на квазилинейные уравнения.

Лит.: [1] Олейник О. А., Радкевич Е. В., Итоги науки. Математический анализ. 1969, М., 1971, с. 7-252; [2] Смирнов М. М., Вырождающиеся эллиптические и гиперболические уравнения, М., 1966.

А. М. Ильин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.