ВЫРОЖДЕННОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ

ВЫРОЖДЕННОЕ ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ - линейное интегральное уравнение Фредгольма с вырожденным ядром. Общий вид В. и. у.:

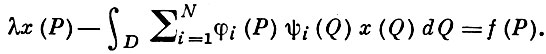
(1)

Интегрирование производят по области D (вообще n-мерного) евклидова пространства, Р и Q - точки из D, λ - действительный или комплексный параметр, а функции, входящие в (1), суммируемы с квадратом на D. Решение В. и. у. (1) ищется в виде

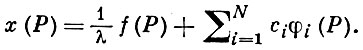
Коэффициенты c_i находятся из системы линейных алгебраич. уравнений

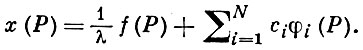
(2)

Если система (2) при заданном X имеет единственное решение, то уравнение (1) также однозначно разрешимо. Те значения λ ≠ 0 (их не более N), при к-рых определитель системы (2) равен 0, являются собственными значениями. Условия разрешимости В. и. у. (1) даются Фредгольма альтернативой. При λ = 0 В. и. у. (1) есть уравнение Фредгольма I рода; для его разрешимости необходимо и достаточно, чтобы функция f могла быть представлена в виде линейной комбинации функций φ_i. Тогда В. и. у. (1) имеет решение, представимое в виде

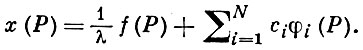
при этом коэффициенты d_j определяются однозначно, а ψ есть функция, удовлетворяющая условиям

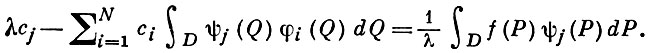
Важность В. и. у. для общей теории уравнений Фредгольма обусловлена тем, что решение любого уравнения Фредгольма II рода может быть с любой точностью в среднем квадратическом (и в нек-рых других метриках) приближено решениями В. и. у. Их вырожденные ядра в том или ином смысле аппроксимируют ядро исходного уравнения.

Абстрактным аналогом и обобщением В. и. у. служит линейное операторное уравнение вида

λх - Ax = f,

где х и f принадлежат банахову пространству Е, а оператор А имеет конечномерную область значений. Свойства таких уравнений аналогичны свойствам В. и. у. (1).

Лит.: [1] Михлин С. Г., Лекции по линейным интегральным уравнениям, М., 1959.

А. Б. Бакушинский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.