ВЫРОЖДЕННОЕ ГИПЕРБОЛИЧЕСКОЕ УРАВНЕНИЕ

ВЫРОЖДЕННОЕ ГИПЕРБОЛИЧЕСКОЕ УРАВНЕНИЕ - дифференциальное уравнение с частными производными

F(t, х, Du) = 0, (*)

где функция F(t, x, q) удовлетворяет условию: корни многочлена

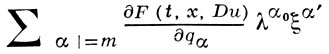
действительны при всех действительных ξ и существуют ξ ≠ 0, t,x и Du, при к-рых либо нек-рые корни совпадают, либо коэффициент при λ^m обращается в нуль. Здесь: t -независимая переменная, часто интерпретируемая как время; х есть n-мерный вектор (x₁, ..., x_n); u(t, x) - искомая функция; α и α'- мультииндексы α = (α₀, ..., α_n), α' = (α₁, ..., α_n); Du - вектор с компонентами

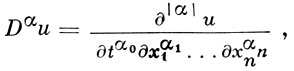
причем в уравнение (*) входят производные порядка не выше m; q_α - компоненты вектора q; ξ есть n-мерный вектор (ξ₁, ..., ξ_n) и ξ^α' = ξ^α'₁, ..., ξ^α'_n.

См. также ст. Вырожденное уравнение с частными производными и лит. при ней.

А. М. Ильин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.