ВЫРОЖДЕННАЯ ИГРА

ВЫРОЖДЕННАЯ ИГРА - бескоалиционная игра n лиц, в к-рой функция выигрыша K_i(х₁, ..., х_n) каждого игрока i вырождена, т. е. имеет вид

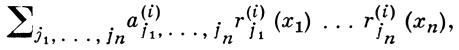
где r⁽ⁱ⁾_jk(x_k), 1 ≤ j_k ≤ n^(k) - функции, заданные на множестве чистых стратегий X_k игрока k, k = 1, ..., n. В случае антагонистических В. и. на единичном квадрате функция выигрыша K(х, у) игрока I равна

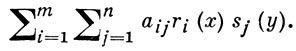
Такая игра сводится к конечной антагонистической выпуклой игре 〈R, S, K〉, где R - выпуклое множество, натянутое на расположенную в m-мерном пространстве кривую r_i = r_i(x), 0 ≤ х ≤ 1, i = 1, ..., m, a S - выпуклое множество, натянутое на кривую s_j = s_j(y), 0 ≤ y ≤ 1, j = 1, ..., n, лежащую в n-мерном пространстве; функция выигрыша К(r, s) имеет вид

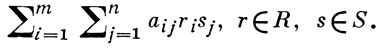
В частности, если r_i(x) = xⁱ, a s_j(y) = y^j, то В. и. наз. полиномиальной игрой. Во всякой антагонистической В. и. на единичном квадрате игрок I имеет оптимальную смешанную стратегию, носитель к-рой состоит не более чем из т точек, если же игра полиномиальная, то не более чем из m/2 точек (при подсчете числа точек концевой точке отрезка приписывается вес 1/2). Аналогично, игрок II имеет оптимальную смешанную стратегию, носитель к-рой состоит не более нем из n точек; в случае полиномиальной игры - не более чем из n/2 точек.

Лит.: [1] Дрешер М., Карлин С., Шепли Л. C., в кн.: Бесконечные антагонистические игры, М., 1963, с. 154-179.

Г. Н. Дюбин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.