ВЫПУКЛЫЙ ФУНКЦИОНАЛ

ВЫПУКЛЫЙ ФУНКЦИОНАЛ - функционал, определенный на векторном линейном пространстве и обладающий тем свойством, что его надграфик является выпуклым множеством. Функционал f, не принимающий значений, равных -∞ на выпуклом множестве А, будет выпуклым на А тогда и только тогда, когда выполняется неравенство

f((1 - α)x + αу) ≤ (1 - α)f(x) + αf(у), х, y ∈ A, 0 ≤ α ≤ 1.

При обратном знаке неравенства функционал f наз. вогнутым. Операциями, переводящими В. ф. в В. ф., являются, напр., сложение (f₁ + f₂)(x) = f₁(x) + f₂(x), умножение на положительное число, взятие верхней грани

(f₁ ∨ f₂)(х) = max(f₁(х), f₂(х)),

инфимальная конволюция

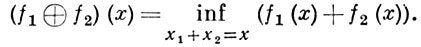
В. ф., ограниченный сверху в окрестности нек-рой точки х, является непрерывным в этой точке. Если В. ф. конечен в нек-рой точке х, то он имеет производную по любому направлению (конечную или бесконечную) в этой точке. Замкнутые В. ф. (т. е. функционалы с выпуклыми и замкнутыми надграфиками) в локально выпуклых линейных топологич. пространствах допускают двойственное описание: они являются верхними гранями аффинных функций, их не превосходящих. Такая двойственность позволяет связать с каждым В. ф. двойственный объект, сопряженный функционал:

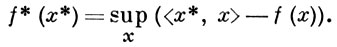
Свойства В. ф., операции над ними, взаимосвязи В. ф. и их сопряженных и т. п. изучаются в выпуклом анализе.

Лит.: [1] Вurnbaum Z., Orlicz W., «Stud. math.», 1931, v. 3, p. 1-67; [2] Харди Г., Литтльвуд Дж. E., Полиа Г., Неравенства, пер. с англ., М., 1948; [3] Красносельский М. А., Рутицкий Я. В., Выпуклые функции и пространства Орлича, М., 1958; [4] Fеnсhеl W., «Саn. J. Math.», 1949. v. 1, p. 73-77; [5] Рокафеллар Р., Выпуклый анализ, пер. с англ., М., 1973.

В. М. Тихомиров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.