ВЫПУКЛОСТЬ

ВЫПУКЛОСТЬ - термин, используемый в разных разделах математики и указывающий на свойства, обобщающие отдельные свойства выпуклых множеств в евклидовых пространствах Еⁿ. С термином «В.» ассоциируется применимость ряда приемов исследования.

В Еⁿ эквивалентны следующие два основных определения. Множество выпукло: а) если оно есть пересечение открытых полупространств; б) если вместе с любыми двумя точками оно содержит соединяющий их отрезок. Оба определения В. переносятся на случай векторных пространств L.

Определение б) распространяют на множества в пространствах с геодезическими (пространства со связностью; локально компактные метрич. пространства, в частности римановы и финслеровы пространства). При этом роль отрезков играют геодезические; но если две точки соединимы не единственной геодезической или кратчайшей, то понятие «В.» разветвляется. В римановой геометрии употребительны, в частности, следующие варианты В. (см. [1]; [2]): 1) множество М выпукло, если каждые две точки из М соединимы единственной кратчайшей и она лежит в М; 2) множество М локально выпукло, если каждая точка из М имеет выпуклую в смысле 1) окрестность в М; 3) множество М слабо выпукло, если каждые две точки соединимы хотя бы одной кратчайшей, идущей в M; 4) множество М абсолютно выпукло, если для каждых двух точек в M лежат все соединяющие их геодезические.

В Еⁿ границу (или часть границы) n-мерного выпуклого тела наз. выпуклой гиперповерхностью, при n = 3 - выпуклой поверхностью, при n = 2 - выпуклой кривой.

Для функции действительного переменного В. означает В. ее надграфика (см. Выпуклая функция действительного переменного). Аналогично определяют В. функционала f в L (см. Выпуклый функционал).

Для выпуклых множеств в L можно говорить о В. семейства 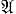множеств, требуя, чтобы из условия М₁, M₂ ∈ 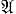, 0 ≤ α ≤ 1 следовало (1 - α)M₁ + αМ₂ ∈ 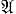. На выпуклых семействах 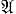определяют выпуклые (и вогнутые) функционалы Ф(М). Выпуклость функционала определяется требованием

Ф((1 - α)M₁ + αM₂) ≤ (1 - α)Ф(М₁) + αФ(М₂).

Термин «В.» для однолистных функций комплексной переменной имеет особый смысл - свойство отображать единичный круг в выпуклую область (см. Выпуклая функция комплексного переменного).

Из обобщений В. в Eⁿ рассматривалась R - выпуклость компакта М, означающая, что каждая точка, удаленная от М менее чем на R, имеет в М единственную ближайшую (см. [4], [5]).

В теории линейных дифференциальных операторов термин «В.» связывают с нек-рыми свойствами групп гомологии [6]. Это ассоциируется с возможностью коснуться границы изнутри области гиперповерхностью, у к-рой определенное число главных кривизн положительно. В теории функций многих комплексных переменных важную роль играет голоморфная выпуклость, связанная с невозможностью коснуться границы области изнутри аналитич. поверхностью [7]. Последнее понятие есть частный случай так наз. К-выпуклости (см. [7], с. 6). В схему K-выпуклости укладываются многие из перечисленных понятий В.

В выпуклом анализе используют понятие Н-выпуклости, обобщающее представимость выпуклой функции как супремума семейства линейных функций [8].

В теории метрич. пространств выпуклость метрики (по Менгеру) определяется как существование для любых точек х ≠ у отличной от них точки, для к-рой ρ(х, у) = ρ(х, z) + ρ(z, х) (см. [9]). Под d - выпуклостью множества М понимают принадлежность М любой такой точки z при х, у ∈ М. Весьма близки к этому определения В. в пространствах с упорядочением (см., напр., Выпуклая подгруппа).

Почти каждому определению В. соответствует связанное с ним понятие локальной В. Но при выделении класса локально выпуклых векторных топологич. пространств термин «локальная В.» имеет особый смысл, означая существование у каждой точки базисной системы выпуклых окрестностей.

Лит.: [1] Громол Д., Клингенберг В., Мейер В., Риманова геометрия в целом, пер. с нем., М., 1971; [2] Александров А. Д., Залгаллер В. А., Двумерные многообразия ограниченной кривизны [Тр. Матем. ин-та АН СССР, т. 63], М., 1962; [3] Xадвигер Г., Лекции об объеме, площади поверхности и изопериметрии, пер. с нем., М., 1966; [4] Fеdеrеr Н., «Trans. Amer. Math. Soc.», 1959, v. 93, №3, p. 418-91; [5] Peшeтняк Ю. Г., «Матем. сб.», 1956, т. 40, с. 381-98; [6] Паламодов В. П., Линейные дифференциальные операторы с постоянными коэффициентами, М., 1967; [7] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [8] Кутателадзе С. С., Рубинов A.M., «Успехи матем. наук», 1972, т. 27, № 3, с. 127-176; [9] Данцер Л., Грюнбаум Б., Кли В., Теорема Хелли и ее применения, пер. с англ., М., 1968.

Ю. Д. Бураго, В. А. Залгаллер.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.