ВЫНУЖДЕНИЯ МЕТОД

ВЫНУЖДЕНИЯ МЕТОД, форсинг-метод, - особый способ доказательства существования моделей аксиоматич. теорий, предложенный П. Коэном в 1963 для доказательства совместимости отрицания континуум-гипотезы ⏋CH и других теоретико-множественных предложений с аксиомами системы Цермело-Френкеля ZF (см. [1]). В дальнейшем В. м. был упрощен и модернизирован (см. [2]-[6]); выявилась, в частности, связь этого метода с теорией булевозначных моделей (см. [2], [3]) и моделями Крипке (см. [6]).

Центральным понятием В. м. является отношение вынуждения

p ⊩ φ

(«условие р вынуждает формулу φ»).

Определению отношения вынуждения предшествует фиксирование нек-рого языка L и частично упорядоченного множества Р вынуждающих условий р с отношением порядка ≤. Язык L может содержать переменные и константы разных сортов (или типов).

Построение модели ZF, предложенное П. Коэном, в к-рой нарушается континуум-гипотеза, выглядит следующим образом. Множество М наз. транзитивным, если

х ∈ М → х ⊆ М.

Пусть М - счетное транзитивное множество, являющееся моделью ZF, и λ ∈ М - ординальное (по Нейману) число, т. е. λ = {α : α < λ}. Пусть A ⊆ λ × ω₀ - произвольное множество (возможно, что А ∉ М), где ω₀ - первое бесконечное ординальное число. Если X - транзитивное множество, то пусть Def (X) обозначает множество всех X-определимых подмножеств (см. Конструктивное по Гёделю множество), т. е. Def (X) = Def (X, ∈ |X). С помощью процесса, аналогичного построению конструктивных по Гёделю множеств, для каждого ординального числа α индуктивно определяется множество М_α[А]:

M_α[A] = ∪_β<α Def (M_β[A]) ∪ {x ∈ M ∪ {A}: x ⊆ M_β[A]}.

Пусть М[А] = М_α0[А], где α₀ = sup {α ∈ М : α - ординал}. Модель ZF, в к-рой нарушается континуум-гипотеза, ищется среди моделей вида М[А]. Пусть λ - ординал такой, что в М истинно утверждение: λ есть второй несчетный ординал.

Множество вынуждающих условий Р и отношение ≤ определяются эквивалентностями: а) р ∈ Р ⇔ p - функция, определенная на нек-ром конечном подмножестве множества λ × ω₀ значениями в множестве {0, 1}, b) p ≤ q ⇔ q есть продолжение р. В качестве языка L берется так наз. разветвленный язык, имеющий много типов переменных (для каждого α ≤ α₀ свой тип переменных, пробегающих множество М_α[А]) и содержащий имена (т. е. индивидные константы) для каждого множества из М[А]. Если х ∈ М, то имя х обозначается через хˇ. Пусть α - имя множества А. Отношение вынуждения р ⊩ φ вводится индуктивным определением, имеющим, в частности, следующие характерные пункты:

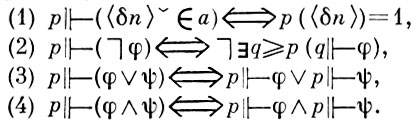
Если α - тип переменной х, то

где С_α - множество всех констант типа α.

Последовательность вынуждающих условий

p₀ ≤ p₁ ≤ p₂ ≤ ... ≤ p_n ≤ ...

наз. полной, если для всякой замкнутой формулы φ языка L имеет место

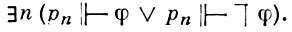
Счетность множества всех замкнутых формул языка L и пункт (2) определения отношения вынуждения позволяют доказать существование полной последовательности, начиная с любого р₀.

Множество А, содержащееся в λ × ω₀, наз. генерическим относительно модели М, если существует такая полная последовательность, что ∪_n≤ω0 p_n есть характеристич. функция χ_A множества А. Фундаментальное значение имеют следующие два факта о генерических множествах и отношении вынуждения.

I. Если А - генерическое множество, то

М[А] ⊨ φ ⇔ ∃p ⊆ χ_A(р ⊩ φ),

где М[A] ⊨ φ означает, что формула φ истинна в М[А].

II. Отношение

p ⊩ φ(c₁, ..., c_n),

где c₁, ..., c_n - константы L, рассматриваемое как отношение между р, c₁, ..., c_n, выразимо в модели М.

В силу этих фактов, для доказательства того, что М[A] ⊨ φ, достаточно показать истинность в модели М утверждения

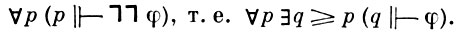
На этом основана проверка справедливости в модели М[А] аксиом ZF и ⏋СН. При проверке ⏋СН в М[А] используется также специфика множества вынуждающих условий, позволяющая доказать, что:

1) если ординалы δ₁, δ₂ < λ различны, то

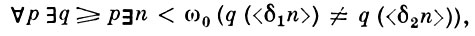
т. е.

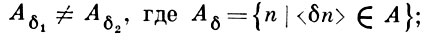
2) М [A] ⊨ (λ есть второй несчетный ординал). Укажем, как отношение вынуждения связано с булевозначными моделями. Если ввести обозначения

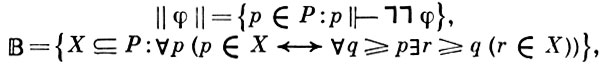
то (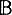, ⊆) есть полная булева алгебра и ||φ|| ∈ 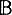есть булево значение формулы φ. Таким образом, задание частично упорядоченного множества (Р, ≤) и определение отношения р ⊩ ⏋⏋φ оказываются равносильными построению нек-рой булевознаяной модели 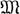. Анализ доказательства утверждений вида:

M[A] ≅ φ₀,

где φ₀ - аксиома ZF или ⏋СН, позволяет заключить, что формулы ZF, выражающие утверждение:

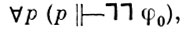
т. е. ||φ|| = 1_B, выводимы из аксиом ZF. Таким образом, 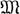есть B-модель для ZF + ⏋CH, построенная средствами ZF. Предположение о существовании счетного транзитивного множества, являющегося моделью ZF, равно как и понятие генерического множества, оказываются несущественными для целей доказательства относительной непротиворечивости.

Выяснилось, что построение булевозначной модели можно упростить (см. [2], [3], [5]). В частности, введение разветвленного языка L не является обязательным. Возможен следующий способ построения генерической модели М[А] (см. [4]).

Подмножество X частично упорядоченного множества (Р, ≤) наз. плотным, если

∀p ∃q ≥ p (q ∈ X).

Пусть Р и отношение ≤ суть элементы нек-рого счетного транзитивного множества М, являющегося моделью ZF. Подмножество G ⊆ P наз. M-генерическим фильтром, если:

1) p ∈ G ∧ q ≤ p → q ∈ G,

2) p ∈ G ∧ q ∈ G → ∃r ∈ G(p ≤ r ∧ q ≤ r),

3) (X ∈ М ∧ X плотно на P) → X ∩ G ≠ ∅.

Пусть G есть М-генерический фильтр на Р. Так как М счетно, то G существует. Вообще говоря, G ∉ M. Отношение ∈_G определяется эквивалентностью

х ∈ _Gy ↔ ∃р ∈ G (〈хр〉 ∈ у),

где х и у - произвольные элементы модели М. Пусть функция F_G определена на М равенством

F_G(y) = {F_G(х): х ∈ _Gy}

и

N_G = {F_G(x): x ∈ М}.

Если φ - замкнутая формула языка ZF, пополненного константами для обозначения каждого множества из М, то положим

р ⊩ φ ↔ ∀ G ∋ p (G есть M-генерический фильтр → N_G ⊨ φ).

Можно показать, что

I. N_G ⊨ φ ↔ ∃р ∈ G(р ≅ φ).

II. Отношение р ≅ φ(с₁, ..., с_n) определимо в модели М для каждой формулы φ.

Используя только I, II и тот факт, что М - модель ZF, можно установить, что N_G - модель ZF. Если Р определено эквивалентностями (а) и (b), то N_G ≄ ⏋СН и ∪G есть характеристич. функция нек-рого множества A ⊆ λ × ω₀ и М[A] = N_G. Определимое в М отношение р ≅ φ не удовлетворяет пунктам (3) и (5) определения П. Коэна отношения вынуждения. Имеет место

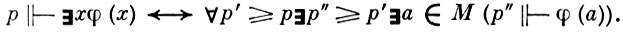
Полагая

||φ|| = {p ⊩ φ}

получим определимую в М булевозначную модель для ZF + ⏋CH с той же булевой алгеброй 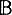, что и в случае П. Коэна.

Таким образом, В. м. состоит фактически в построении 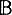-модели и гомоморфизма, сохраняющего нек-рые бесконечные объединения и пересечения алгебры 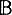, в двухэлементную алгебру {0, 1} (о применениях В. м. в теории множеств см., напр., [2]).

Лит.: [1] Коэн П. Дж., Теория множеств и континуум-гипотеза, пер. с англ., М., 1969; [2] Йех Т., Теория множеств и метод форсинга, пер. с англ., М., 1973; [3] Takeuti G., Zaring W. М., Axiomatic set theory, N. У.-Hdlb.-В., 1973; [4] Шенфилд Дж., Математическая логика, пер. с англ., М., 1975; [5] Манин Ю. И., в кн.: «Итоги науки и техники. Современные проблемы математики, т. 5, М., 1975, с. 5-72; [6] Fitting М. С., Intuitionistic logic. model theory and forcing, Amst.-L., 1969.

В. H. Гришин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.