ВЫМЕТАНИЯ МЕТОД

ВЫМЕТАНИЯ МЕТОД - метод решения Дирихле задачи для Лапласа уравнения, развитый А. Пуанкаре (см. [1], [2], а также [4]) и состоящий в следующем. Пусть D - ограниченная область евклидова пространства ℝⁿ, n ≥ 2, Г = ∂D - граница D. Пусть δ_y - мера Дирака, сосредоточенная в точке y ∈ D; U(x; δ_y) -ньютонов потенциал меры δ_y при n ≥ 3 или логарифмический потенциал меры δ_y при n = 2. Выметанием меры δ_y из области D на границу Г наз. такая мера β_y, на Г, потенциал к-рой U(х; β_y) совпадает вне D с U(x; δ_y), а внутри D не превосходит U(х; δ_y); эта мера β_y единственна и совпадает с гармонической мерой на Г для точки y ∈ D. Аналогично определяется выметание произвольной положительной меры, сосредоточенной на D. Если D - шар, то плотность распределения масс β_y, т. е. производная меры β_y, есть не что иное, как ядро Пуассона (см. Пуассона интеграл). Вообще, если граница Г достаточно гладкая, то мера β_y абсолютно непрерывна и плотность распределения масс β_y совпадает с нормальной производной Грина функции для D. При помощи меры β_y решение задачи Дирихле записывается в виде так наз. формулы Валле Пуссена:

U(y) = ∫_Г f(x) dβ_y(x),

где f(x) - заданная на Г функция.

А. Пуанкаре в первоначальном изложении В. м. указывал сначала геометрич. конструкцию процесса выметания для шара; затем, опираясь на Гарнака теоремы и на возможность нечерпания области D последовательностью шаров {B_k}^∞_k=1, он строил бесконечную последовательность потенциалов {U_n}^∞_n=1, в к-рой каждый потенциал U_n+1 получается из предыдущего U_n выметанием масс из области ∪ⁿ_k=1B_k на ее границу и к-рая сходится к решению задачи Дирихле для достаточно гладкой области D (подробное исследование условий применимости В. м. см. в [3]).

В современной теории потенциала (см. [5], [6]) проблема выметания трактуется как самостоятельная задача, близкая к задаче Дирихле, причем оказывается возможным рассматривать выметания мер на множества довольно общей природы. Таким образом, в простейшей постановке проблема выметания состоит в нахождении по заданному распределению масс р внутри замкнутой области D̄ такого распределения масс ν на Г = ∂D, чтобы вне D̄ потенциалы обоих распределений совпадали. Решением этой проблемы выметания меры μ в случае гладкой границы Г будет абсолютно непрерывная мера ν. Ее плотность, или производная ν'(у), у ∈ Г, записывается при помощи функции Грина G(x, у) области D в виде

(*)

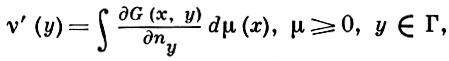
где ∂G/∂n_y - производная от G(x, у) по направлению внутренней нормали к Г в точке у ∈ Г. Внутри области D для потенциалов имеет место неравенство U(х; ν) ≤ U(х; μ), т. е. при выметании внутри области потенциал может только убывать. Если μ = δ_x - мера Дирака, сосредоточенная в точке x ∈ D, то формула (*) дает ν'(y) = ∂G(x, y)/∂n_y, т. е. нормальная производная функции Грина есть плотность меры, полученной выметанием единичной массы, сосредоточенной в точке x ∈ D. Обобщая формулу (*), получают выражение выметенной меры ν(Е) любого борелевского множества Е ⊂ Г в случае произвольной области D:

ν(Е) = ∫ ω(х; Е, D) dμ(x),

где ω(х; Е, D) - гармоническая мера множества Е относительно области D в точке х.

Если К - произвольный компакт в ℝⁿ, а μ - ограниченная положительная борелевская мера, то выметанием меры μ на компакт K наз. такая мера ν, сосредоточенная на K, что всюду U(х; ν) ≤ U(х; μ) и квазивсюду на K, т. е. за возможным исключением множества точек внешней емкости нуль, U(x; ν) = U(x; μ). Эта постановка проблемы выметания, более общая по сравнению с выметанием из области, распространяется и на потенциалы других видов, напр. на бесселевы потенциалы, Рисса потенциалы. Рассматриваются также выметания мер на произвольные борелевские множества K.

Близкой к этой постановке является проблема выметания для супергармонических функций. Пусть v - неотрицательная супергармонич. функция в области D ⊂ ℝⁿ. Выметанием для функции v на компакт K ⊂ D̄ наз. наибольшая супергармонич. функция В^K_v такая, что: 1) ее ассоциированная мера сосредоточена на K; 2) всюду В^K_v ≤ v; 3) B^K_v= v квазивсюду на K.

В потенциала теории абстрактной проблема выметания в обеих постановках получает решение для множеств К в произвольных гармонических пространствах X, т. е. в таких локально компактных топологич. пространствах X, к-рые допускают выделение аксиоматически определенного пучка гармонич. функций. Этот аксиоматич. подход позволяет рассматривать проблему выметания для потенциалов, связанных с дифференциальными уравнениями с частными производными более общей природы (см. [7]).

Лит.: [1] Pоinсaré Н., «Аmеr. J. Math.», 1890, v. 12, № 3, p. 211-94; [2] его же, Théorie du potentiel Newtonien, P., 1899; [3] La Vallée-Pоussin Сh. J. de, Le potentiel logarithmique, balayage et répresentation conforme, Louvain-P., 1949; [4] Сретенский Л. H., Теория ньютоновского потенциала, М.-Л., 1946; [5] Ландкоф Н. С., Основы современной теории потенциала, М., 1966; [6] Брело М., Основы классической теории потенциала, пер. с франц М., 1964; [7] Constantinescu С., Cornea A., Potential theory on harmonic spaces, В., 1972.

E. Д. Соломенцев

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.