ВЫБОРОЧНАЯ ФУНКЦИЯ

ВЫБОРОЧНАЯ ФУНКЦИЯ - функция X_t = X_t(ω) аргумента t, однозначно соответствующая каждому наблюдению случайного процесса X_t ∈ Е, t ∈ T; здесь {ω} = Ω - множество элементарных событий. Часто используются эквивалентные В. ф. термины «реализация», «траектория». Случайный процесс X_t характеризуется вероятностной мерой в пространстве В. ф. При изучении локальных свойств В. ф. X_t (где E = ℝ¹, Т = ℝ^m - евклидово пространство размерности m = 1, 2, ...) предполагается, что X_t является сепарабельным или находится эквивалентный случайный процесс с заданными локальными свойствами В. ф. Наиболее полно исследованы локальные свойства В. ф. гауссовских процессов.

Для стационарных гауссовских случайных процессов (полей) X_t имеет место альтернатива: почти все В. ф. X_t либо непрерывны, либо неограничены на любом интервале. Для t, s ∈ T определено «расстояние» d(t, s) = [E|X_t - X_s|²]^1/2, B(t, δ) = {s : d(s, t) ≤ δ} - «сфера», N(δ) - минимальное число таких «сфер», покрывающих Т ⊂ ℝⁿ, sup_s,t∈T d(s, t) < ∞. Необходимое и достаточное условие непрерывности В. ф. однородного гауссовского процесса имеет вид

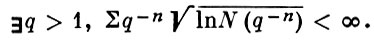
Если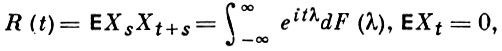

выпукла вниз в нек-рой окрестности точки +0, то для непрерывности В. ф. X_t необходимо и достаточно, чтобы Σ S^1/2_n < ∞, где S_n = F(2ⁿ⁺¹) - F(2ⁿ). Если R(t) выпукла вниз в окрестности +0 и

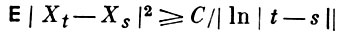
для |t - s| < δ, то почти все В. ф. гауссовского случайного процесса X_t неограничены. Если

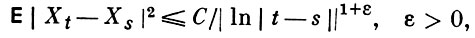
то почти все В. ф. гауссовского случайного процесса (поля) X_t непрерывны. Для непрерывности В. ф. гауссовского случайного процесса достаточно, чтобы

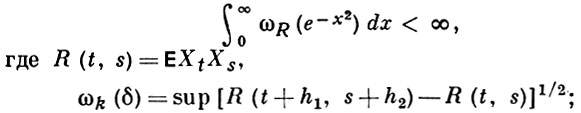
здесь sup берется по |h_i| < δ, |t| ≤ C, |s| ≤ C. В. ф. X_t, t ∈ ℝⁿ относят к классу H(С, α₁, ..., α_n), если для всех достаточно малых h_i

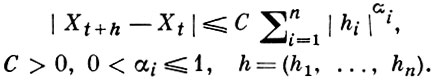
Если ξ_t - гауссовское случайное поле на единичном кубе V⁰_n в ℝⁿ такое, что для достаточно малых h И t ∈ V⁰_n

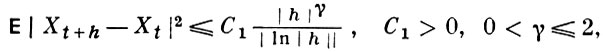
то с вероятностью, равной 1, равномерно по t ∈ V⁰_n

X_t ∈ H(C, β₁, ..., β_n)

для любого С > 0 и β_i ≤ γ/2.

Неубывающая непрерывная функция φ(х), x ∈ ℝ¹, наз. верхней, если для почти всех со существует ε = ε(ω) такое, что

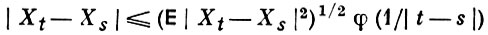
при 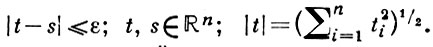Если X_t - гауссовское случайное поле, 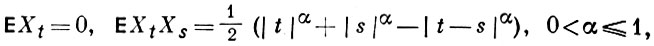то φ(х) является верхней тогда и только тогда, когда

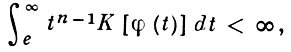
где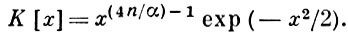

Для того чтобы почти все В. ф. гауссовского случайного процесса были аналитическими в окрестности точки t₀, необходимо и достаточно, чтобы ковариационная функция R(t, s) была аналитической по t и s в окрестности |t - t₀| < δ, |s - t₀| < δ, δ > 0.

Лит.: [1] Дуб Дж., Вероятностные процессы, пер. с англ., М., 1956; [2] Крамер Г., Лидбеттер М., Стационарные случайные процессы, пер. с англ., М., 1969- [3] Беляев Ю. К., в кн.: Proceeding of the 4 Berkeley Symposium on Mathematical Statistics and Probability v. 2, Berk.-Los Ang., 1961, p. 23-33; [4] Остpовский Е. И., «Докл. АН СССР», 1970, т. 195, № 1, с. 40-42; [5] Nisio Мakikо, «Nogoya Math. J.», 1969, v. 34, p. 89-104; [6] Dudley R. M., «Ann. Math. Statistics», 1965, v. 36, № 3, p. 771-88; [7] Fernique X., «C. r. Acad. sci.», 1964, t. 258, p. 6058-60; [8] Ядренко M. Й., «Вiсник Киiвського ун-ту. Сер. матем. та механ.», 1967, т. 9, с. 103-12; [9] Kawadа Takayuki, «Nagoya Math. J.», 1969, v. 35, p. 109-32; [10] Беляев Ю. К., «Теория вероят. и ее примен.», 1959, т. 4, № 4, с. 437-44; [11] Слуцкий Е. Е., «Giorn. Inst Ital. Attuari», 1937, v. 8, № 2, p. 3-19; [12] Fernique X., в кн.-Ecole d'Ete de Probabilités de Saint-Flour IV-1974, В.-Hdlb.-N. Y., 1975, p. 1-96 («Lecture Notes in Mathematics», № 480).

Ю. К. Беляев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.