ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА

ВТОРАЯ КВАДРАТИЧНАЯ ФОРМА поверхности - квадратичная форма от дифференциалов координат на поверхности, к-рая характеризует локальную структуру поверхности в окрестности обыкновенной точки. Пусть поверхность задана уравнением

r = r(u, v),

где u и v - внутренние координаты на поверхности;

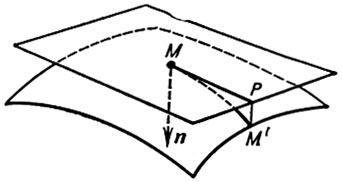
dr = r_udu + r_vdv - дифференциал радиус-вектора r вдоль выбранного направления du/dv смещения из точки М в точку М' (см. рис.);

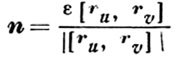
- единичный вектор нормали к поверхности в точке М (здесь ε = +1, если тройка векторов {r_u, r_v, n} правой ориентации, и ε = -1 в противоположном случае). Удвоенная главная линейная часть 2δ отклонения РМ' точки М' поверхности от касательной плоскости в ее точке М равна

II = 2δ = (-dr, dn) = (r_uu, n) du² + 2(r_uv, n) du dv + (r_vv, n) dv²;

она и наз. второй основной квадратичной формой поверхности.

Коэффициенты В. к. ф. обычно обозначают через

L = (r_uu, n), M = (r_uv, n), N = (r_vv, n)

или в тензорных символах

(-dr, dn) = b₁₁ du² + 2b₁₂ du dv + b₂ dv².

Тензор b_ij наз. вторым основным тензором поверхности.

О связи В. к. ф. с другими квадратичными формами поверхности и лит. см. Квадратичные формы поверхности.

А. Б. Иванов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.