ВТОРАЯ ВАРИАЦИЯ

ВТОРАЯ ВАРИАЦИЯ - частный случай n-той вариации функционала (см. также Гато вариация), обобщающий понятие второй производной функции нескольких переменных; используется в вариационном исчислении. Согласно общему определению В. в. в точке х₀ функционала f(x), определенного в нормированном пространстве X, есть

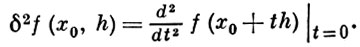
При равенстве нулю первой вариации неотрицательность В. в. является необходимым, а строгая положительность

δ² f(x₀, h) ≥ α ||h||², α > 0

при нек-рых допущениях - достаточным условием локального минимума f(x) в точке х₀.

В простейшей (векторной) задаче классического вариационного исчисления В. в. функционала

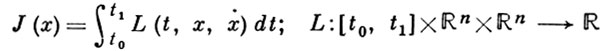
(рассматриваемого на векторных функциях класса С¹ с закрепленными краевыми значениями x(t₀) = x₀, x(t₁) = x₁) имеет вид:

(*)

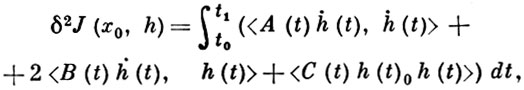
где 〈⋅, ⋅〉' означает стандартное скалярное произведение в ℝⁿ, a A(t), B(t), C(t) - матрицы с коэффициентами 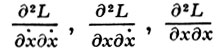соответственно (производные вычисляются в точках кривой x₀(t)). Целесообразно рассматривать функционал от h, определяемый формулой (*), не только в пространстве С¹, но и на более широком пространстве W¹₂ абсолютно непрерывных векторных функций с интегрируемым квадратом модуля производной. В этом случае неотрицательность и строгая положительность В. в. формулируются в терминах неотрицательности и строгой положительности матрицы A(t) (Лежандра условие) и отсутствия сопряженных точек (Якоби условие), что дает условия слабого минимума в вариационном исчислении.

Для вариационного исчисления в целом было проведено исследование В. в. для экстремалей, не обязательно доставляющих минимум (однако, по-прежнему, -при выполнении условия Лежандра, см. [1]). Важнейший результат - совпадение Морса индекса В. в. и числа точек, сопряженных с t₀, на интервале (t₀, t₁) (см. [2]).

Лит.: [1] Morse М., The calculus of variations in tne large, N. Y., 1934; [2] Милнор Дж., Теория Морса, пер. с англ., М., 1965.

В. М. Тихомиров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.