ВРОНСКИАН

ВРОНСКИАН, определитель Вроньского, - определитель системы n вектор-функций размерности n

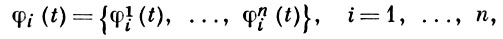
(1)

имеющий вид:

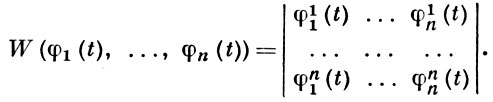
В. системы n скалярных функций

f₁(t), ..., f_n(t), (2)

имеющих производные до (n-1)-го порядка включительно, есть определитель

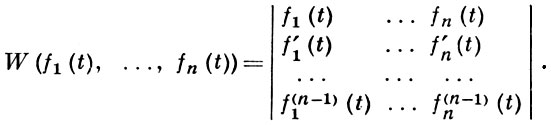
Это понятие было введено Ю. Вроньским [1].

Если вектор-функции (1) линейно зависимы на множестве Е, то

W(φ₁(t), ..., φ_n(t)) ≡ 0, t ∈ Е;

если скалярные функции (2) линейно зависимы на множестве Е, то

W(f₁(t), f_n(t)) ≡ 0, t ∈ Е.

Обратные утверждения, вообще говоря, неверны: тождественное обращение В. в нуль на нек-ром множестве не является достаточным условием линейной зависимости n функций на этом множестве.

Пусть вектор-функции (1) суть решения линейной однородной системы n-го порядка х' = А(t)x с непрерывной на интервале I(n × n)-матрицей A(t). Если эти решения составляют фундаментальную систему, то

W(φ₁(t), ..., φ_n(t)) ≠ 0, t ∈ I;

Если В. этих решений равен нулю хотя бы в одной точке I, то он тождественно равен нулю на I, а функции (1) линейно зависимы. Имеет место формула Лиувилля:

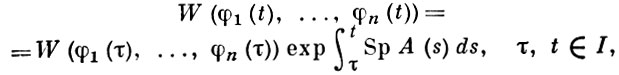
где Sp A(t) - след матрицы A(t).

Пусть функции (2) суть решения линейного однородного уравнения n-го порядка

y⁽ⁿ⁾ + p₁(t) y^(n-1) + ... + p_n-1(t)у' + p_n(t)y = 0

с непрерывными на интервале I коэффициентами. Если эти решения составляют фундаментальную систему, то

W(f₁(t), f_n(t)) ≠ 0, t ∈ I.

Если В. этих решений равен нулю хотя бы в одной точке I, то он тождественно равен нулю на I, а функции (2) линейно зависимы. Имеет место формула Лиувилля:

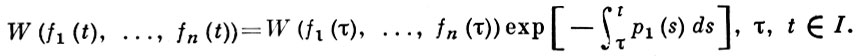
Лит.: [1] Hоёne-Wrоński J., Réfutation de la théorie des fonctions analitiques de Lagrange, P., 1812; [2] Понтрягин Л. С., Обыкновенные дифференциальные уравнения, 4 изд., М., 1974.

Н. X. Розов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.