ВРАЩЕНИЯ ТЕОРЕМЫ

ВРАЩЕНИЯ ТЕОРЕМЫ - теоремы, характеризующие изменение аргумента при конформном отображении. В. т. в классе S функций f(z) = z + c₂z² + ..., регулярных и однолистных в круге |z| < 1, дает точные оценки аргумента производной для функций этого класса:

(*)

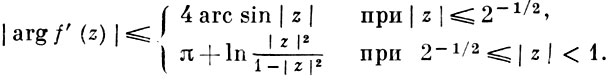
Здесь рассматривается та ветвь arg f'(z), к-рая равна нулю при z = 0. Верхние и нижние границы для arg f'(z), устанавливаемые неравенствами (*), являются точными при любом z из круга |z| < 1. Эта В. т. получена Г. М. Голузиным (см. [1], [5]; точность неравенств (*) при 2^-1/2 < |z| < 1 впервые доказана в [2]; полный анализ случаев равенства в этих оценках дается в [3]).

Теоремами вращения в классе S наз. также оценки arg(f(z)/z) и оценки выражений вида

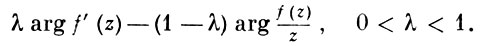
Простейшими оценками такого рода в классе S являются точные неравенства (рассматриваются соответствующие ветви аргументов):

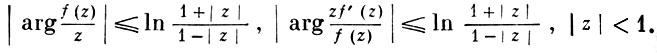
В. т. имеются и в других классах функций, реализующих однолистное конформное отображение круга или его внешности, и в классах функций, однолистных в многосвязной области (см. [5], [3], Искажения теоремы, Однолистная функция). В. т. распространены также на случай р-листных функций (см. Добавления в [5], а также Многолистная функция).

Лит.: [1] Голузин Г. М., «Матем. сб.», 1936, т. 1 (43) в. 1, с. 127-35; [2] Базилевич И. Е., «Матем. сб.», 1936, т. 1 (43), в. 3, с. 283-92; [3] Дженкинс Дж., Однолистные функции и конформные отображения, пер. с англ М., 1962; [4] Grunsky Н., «Schr. Math. Sem. und Inst. für angew. Math. Univ. Berlin», 1932, Bd 1, S. 95-140; [5] Гoлузин Г. M., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966.

Г. В. Кузьмина.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.