ВРАЩЕНИЙ МЕТОД

ВРАЩЕНИЙ МЕТОД, метод Якоби, - метод решения полной проблемы собственных значений эрмитовой матрицы, основанный на подобном преобразовании эрмитовой матрицы к диагональному виду с помощью последовательности плоских вращений. В. м. -итерационный метод, он имеет простую вычислительную схему и всегда сходится, причем скорость сходимости асимптотически квадратичная. Наличие кратных и близких собственных значений у матрицы не вызывает осложнений. В. м. позволяет вычислить собственные значения как с нахождением собственных векторов, так и без них. Система собственных векторов, вычисленная по В. м., ортонормирована.

Идеи В. м. предложены в [1]. В современном виде это один из наиболее развитых и эффективных по реализации на ЭВМ методов решения полной проблемы собственных значений матрицы.

Классический В. м. состоит в построении последовательности матриц А₀, А₁, А₂, ....., где А₀ = А - исходная матрица, А_k = U*_kA_k-1U_k, U_k - матрица плоского вращения, аннулирующего максимальный по модулю внедиагональный элемент матрицы A_k-1. При этом, если 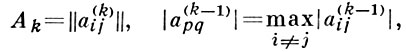, то матрица U_k = ||u^k_ij|| отличается от единичной лишь элементами u^(k)_pp, u^(k)_qq, u^(k)_pq, u^(k)_qp. В действительном случае, когда А - симметрическая матрица,

(*)

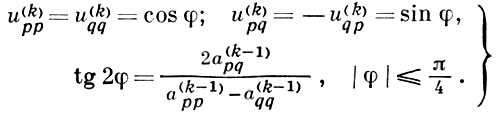
В комплексном случае соотношения (*) незначительно усложняются.

Последовательность матриц A_k сходится к диагональной матрице Λ, скорость сходимости асимптотически квадратичная. Диагональные элементы матрицы Λ являются приближенными собственными значениями А, а столбцы матрицы U^(k) = U₁U₂ ... U_k - приближенными собственными векторами.

Реализация описанного варианта В. м. требует выбора максимального по модулю внедиагонального элемента матрицы на каждом шаге. Для выполнения этой операции на ЭВМ требуется значительный объем вычислительной работы.

Существуют другие варианты В. м., более эффективные в этом отношении: циклич. В. м., В. м. с барьером, В. м. с выбором оптимального элемента.

В циклическом В. м. пары индексов (р, q) аннулирующего элемента пробегают циклически все наддиагональные позиции. Недостатком этого процесса является возможность выполнения большого числа неэффективных вращений, аннулирующих малые внедиагональные элементы.

Этот недостаток частично устраняется в барьерном В. м., в к-ром вводится монотонно убывающая к нулю последовательность чисел α₁, α₂, ...., называемых барьерами, и при циклич. просмотре индексов (р, q) аннулируются лишь те внедиагональные элементы, к-рые по модулю меньше α₁. После того, как все внедиагональные элементы стали меньше α₁ барьер α₁ заменяется на барьер α₂ и процесс продолжается. Практич. использование этого варианта В. м. встречает ряд трудностей, связанных с выбором оптимального барьера.

Наиболее эффективным для использования в вычислительной практике является В. м. с выбором оптимального элемента [4]. В этом методе пары индексов (р, q) соответствуют почти максимальному элементу и выбираются так, что р - номер строки с максимальной евклидовой длиной, q - номер столбца максимального по модулю внедиагонального элемента р-й строки. Поскольку на каждом шаге процесса строки матрицы, за исключением р-й и q-й, не меняют длины, то выбор индексов (р, q) существенно не увеличивает общего объема вычислений. Вся теория классич. В. м. полностью переносится на описанную модификацию [2].

Расчетные формулы В. м., реализующие вычисление (*), обеспечивают сходимость процесса В. м. в реальных условиях машинной арифметики и высокую точность как собственных значений, так и собственных векторов [5].

Лит.: [1] Jacobi С. G. J., «J. reine und angew. Math.», 1846, Bd 30, S. 51-94; [2] Воеводин В. В., Численные методы алгебры, М., 1966; [3] Уилкинсон Дж. X., Алгебраическая проблема собственных значений, пер. с англ М., 1970; [4] Воеводин В. В., Ким Г. Д., Программа для нахождения собственных значений и собственных векторов симметрической матрицы методом вращений, в сб.: Вычислительные методы и программирование, М., 1962, с. 269-77; [5] Ким Г. Д., в сб.: Численный анализ на ФОРТРАН'е, в. 3, М., 1973, с. 97-113.

Г. Д. Ким.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.