ВРАЩЕНИЕ

ВРАЩЕНИЕ - частный случай движения, при к-ром по крайней мере одна точка пространства остается неподвижной. При В. плоскости неподвижная точка наз. центром вращения, при В. пространства неподвижная прямая - осью вращения. В. евклидова пространства наз. собственным (В. 1-го рода), или несобственным (В. 2-го рода) в зависимости от того, сохраняет оно или не сохраняет ориентацию пространства.

На плоскости собственное В. выражается аналитически в декартовых прямоугольных координатах (х, у) при помощи формул (начало координат в центре В.)

х̃ = х cos φ - у sin φ, у̃ = х sin φ + y cos φ,

где φ - угол поворота. Собственное В. на угол φ может быть представлено как произведение двух осевых симметрии с осями, пересекающимися под углом φ/2. Несобственное В. на плоскости выражается аналитически в декартовых прямоугольных координатах (х, у) при помощи формул (начало координат в центре В.):

x̃ = х cos φ + y sin φ, у̃ = х sin φ - у cos φ,

где φ - угол поворота. Несобственное В. на плоскости может быть представлено как произведение собственного В. на осевую симметрию.

В случае n-мерного евклидова пространства В. аналитически выражается с помощью ортогональной матрицы, к-рая приводится к канонич. виду:

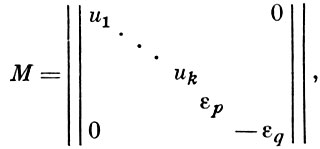
где

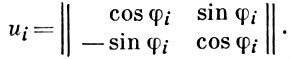
ε_s - единичная матрица порядка s(s = p, q). Возможны следующие случаи:

1) р = n - тождественное преобразование;

2) q = n - В. является центральной симметрией;

3) p + q = n - В. является симметрией относительно р-плоскости (отражением от р-плоскости);

4) М не содержит подматриц ε_p и -ε_q - В. наз. поворотом вокруг единственной неподвижной точки;

5) М содержит подматрицы u_i и ε_p, но не содержит подматрицу -ε_q - В. наз. поворотом вокруг р-плоскости;

6) М содержит подматрицы u_i и -ε_q, но не содержит подматрицы ε_p - В. наз. поворотным отражением от (n - q)-плоскости.

В. евклидова пространства Е_n вокруг данной точки образует группу относительно операции умножения В., изоморфную группе ортогональных преобразований векторного пространства Rⁿ или группе ортогональных матриц порядка n над полем R. Группа В. пространства Е_n является n(n - 1)/2-мерной группой Ли и действует в Е_n интранзитивно.

Лит.: [1] Розенфельд Б. А., Многомерные пространства, М., 1966; [2] его же, Неевклидовы пространства, М., 1969; [3] Широков П. А., Тензорное исчисление. Алгебра тензоров, 2 изд., Казань, 1961.

В. Т. Базылев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.