ВПОЛНЕ РЕГУЛЯРНОЕ ПРОСТРАНСТВО

ВПОЛНЕ РЕГУЛЯРНОЕ ПРОСТРАНСТВО - топологическое пространство, в к-ром всякие два множества, из к-рых одно замкнуто, а другое состоит лишь из одной точки, функционально отделимы (см. Отделимости аксиомы). В. р. п., в к-рых все одноточечные множества замкнуты (т. е. вполне регулярные T₁-пространства), часто наз. тихоновскими пространствами. Они образуют один из важнейших классов топологич. пространств, выделяющийся многими замечательными свойствами и особенно часто встречающийся в приложениях топологии к другим областям математики. Так, напр., пространство всякой топологич. группы является В. р. п., но может не быть нормальным пространством. Все тихоновские пространства являются хаусдорфовыми и могут быть определены как пространства, имеющие (хаусдорфовы) бикомпактные расширения, т. е. как (даже всюду плотные) подпространства бикомпактов. Среди этих расширений данного пространства имеется единственное с точностью до гомеоморфизма максимальное или Стоуна-Чеха бикомпактное расширение, к-рое может быть непрерывно отображено на всякое (хаусдорфово) бикомпактное расширение данного пространства так, что каждая его точка отображается в себя.

Прямое определение тихоновских пространств без привлечения действительных чисел и функций основано (см. [3]) на рассмотрении двух сопряженных баз пространства - открытой ℬ и замкнутой 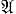, причем сопряженность этих баз означает, что каждая база состоит из множества, дополнительных к множествам, составляющим другую базу. Такая пара {ℬ, 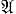} сопряженных баз наз. регулярной, если она удовлетворяет следующим условиям: 1) всякие два дизъюнктные замкнутые множества базы 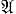имеют дизъюнктные окрестности, принадлежащие ℬ; 2) база 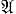является сетью, т. е. для произвольной точки х ∈ Х и ее произвольной окрестности Ох в базе ℬ найдется такой элемент В, что X\x ⊃ B ⊃ X\O(х). Для того чтобы T₁-пространство было вполне регулярным, необходимо и достаточно, чтобы оно обладало хотя бы одной регулярной парой сопряженных баз (теорема Зайцева).

Лит.: [1] Александров П. С., Введение в общую теорию множеств и функций, М.-Л., 1948; [2] Понтрягин Л. С., Непрерывные группы, 3 изд., М., 1970; [3] Келли Дж. Л., Общая топология, пер. с англ., М., 1968; [4] Александров П. С., Пасынков Б. А., Введение в теорию размерности. Введение в теорию топологических пространств и общую теорию размерности, М., 1973; [5] Зайцев В. И., «Вестн. Моск. ун-та. Сер. матем.», 1967, № 3, с. 48-57.

П. С. Александров.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.