ВПОЛНЕ ПРИВОДИМАЯ МАТРИЧНАЯ ГРУППА

ВПОЛНЕ ПРИВОДИМАЯ МАТРИЧНАЯ ГРУППА - матричная группа G над произвольным фиксированным полем Р, все матрицы к-рой одновременным сопряжением посредством нек-рой матрицы над Р можно привести к клеточно-диагональному виду, т. е. к виду

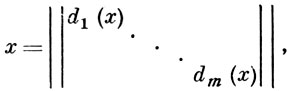
где d_i(x), i = 1, ..., m, - квадратные матрицы, а на остальных местах стоят нули, причем каждая матричная группа d_i(G) неприводима (см. Неприводимая матричная группа). На языке преобразований: группа G линейных преобразований конечномерного векторного пространства V над полем наз. вполне приводимой, если выполнено любое из трех следующих равносильных условий: 1) любое подпространство из V, инвариантное относительно G, имеет прямое дополнение, инвариантное относительно G (см. Инвариантное подпространство); 2) V разлагается в прямую сумму минимальных инвариантных относительно G подпространств; 3) V порождается минимальными инвариантными относительно G подпространствами. Всякая конечная матричная группа G над полем, характеристика к-рого не делит порядок G, вполне приводима. Всякая нормальная подгруппа вполне приводимой матричной группы сама вполне приводима.

Лит.: [1] Мерзляков Ю. И., Рациональные группы, Новосибирск, 1967; [2] Холл М., Теория групп, пер. С англ., М., 1962.

Ю. И. Мерзляков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.