ВПОЛНЕ ИНТЕГРИРУЕМОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ

ВПОЛНЕ ИНТЕГРИРУЕМОЕ ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ - уравнение вида

(*)

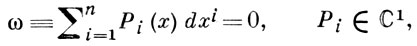
для к-рого через каждую точку нек-рой области в пространстве ℝⁿ проходит (n - 1)-мерное интегральное многообразие. Необходимым и достаточным условием полной интегрируемости дифференциального уравнения (*) является условие Фробениуса ω ∧ dω = 0 (∧ - знак внешнего произведения, см. [1]). Для n = 3 это условие принимает вид:

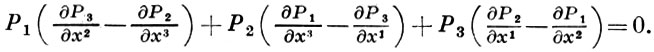
Иногда вместо уравнения (*) рассматривают систему уравнений (см. [2]):

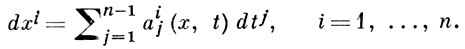
Условия полной интегрируемости в этом случае принимают вид:

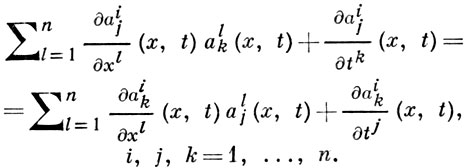
Семейство интегральных многообразий В. и. д. у. представляет собой слоение (см. [3]).

Лит.: [1] Frobenius G., «J. reine und angew. Math.», 1877, Bd 82, S. 230-315; [2] Немыцкий В. В., «Матем. сб.», 1948, т. 23 (65), с. 161-86; [3] Новиков С. П., «Тр. Моск. матем. об-ва», 1965, т. 14. с. 248-78.

Л. Э. Рейзинь.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.