ВОРОНОГО МЕТОД СУММИРОВАНИЯ

ВОРОНОГО МЕТОД СУММИРОВАНИЯ - матричный метод суммирования последовательности; определяется числовой последовательностью {р_n} и обозначается символом (W, р_n). Последовательность {s_n} суммируется методом (W, р_n) к числу S, если

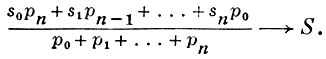
В частности, при р₀ = 1, p_k = 0, k ≥ 1, суммируемость последовательности методом (W, р_n) к числу S означает, что эта последовательность сходится к S. При р_k = 1, k ≥ 0 получается Чезаро метод суммирования. Если р₀ > 0, p_k ≥ 1, k ≥ 1, то метод (W, р_n) является регулярным методом суммирования тогда и только тогда, когда p_n/(p₀ + p₁ + ... + p_n) →0. Два любых регулярных метода (W, р'_n) и (W, р''_n) совместны (см. Совместность методов суммирования).

В. м. с. был впервые введен Г. Ф. Вороным [1] и был переоткрыт в 1919 Н. Э. Нёрлундом (N. Е. Nörlund). Поэтому иногда в зарубежных источниках методы (W, р_n) наз. методами Нёрлунда и обозначаются (N, р_n) или N(р_n).

Лит.: [1] Вороной Г. Ф., в кн.: Дневник одиннадцатого съезда русских естествоиспытателей и врачей, СПБ, 1902, с. 60-61; [21 Харди Г., Расходящиеся ряды, пер. с англ., М., 1951, С. 88-121.

Ф. И. Харшиладзе.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.