ВОЛЬТЕРРА УРАВНЕНИЕ

ВОЛЬТЕРРА УРАВНЕНИЕ - интегральное уравнение вида

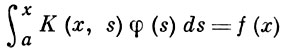
(1)

(линейное интегральное В. у. I рода) или вида

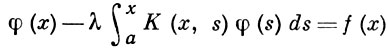
(2)

(линейное интегральное В. у. II рода). Здесь х, s, а - действительные числа, λ (вообще говоря) - комплексный параметр, φ(s) - неизвестная функция, f(x), К(х, s) - заданные функции, суммируемые с квадратом соответственно на отрезке [а, b] и в области a ≤ x ≤ b, a ≤ s ≤ x. При этом функция f(x) наз. свободным членом В. у., а функция К(х, s) -ядром В. у.

В. у. могут рассматриваться как частный вид Фредгольма уравнений, когда ядро К(х, s), задаваемое на квадрате a ≤ x ≤ b, a ≤ s ≤ b, обращается в нуль в треугольнике a ≤ x < s ≤ b. В. у. II рода без свободного члена наз. однородным В. у. Выражение

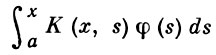
определяет интегральный оператор, действующий в L₂; он наз. Вольтерра оператором.

Впервые уравнения вида (2) были систематически рассмотрены В. Вольтерра [1], [2]. Частный вид В. у. (1) -Абеля интегральное уравнение, был впервые рассмотрен Н. X. Абелем (N. Н. Abel). Основной результат теории В. у. II рода состоит в следующем. При любом комплексном λ ≠ ∞ существует, и притом единственное, суммируемое с квадратом решение В. у. II рода. Это решение может быть получено методом последовательных приближений, т. е. как предел сходящейся в среднем квадратическом последовательности:

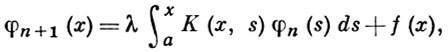
(3)

φ₀- производная, суммируемая с квадратом. В случае непрерывного ядра К(х, s) и f ∈ С([а, b]) эта последовательность сходится равномерно на [а, b] к единственному непрерывному решению.

Относительно В. у. I рода справедливы следующие утверждения. Если f(s) и К(х, s) дифференцируемы, К(х, х) ≠ 0, х ∈ [а, b], и если К(х, х) и К'_x(х, s) суммируемы с квадратом соответственно на [а, b] и на а ≤ х ≤ b, a ≤ s ≤ b, то В. у. I рода эквивалентно В. у. II рода, полученному дифференцированием из В. у. I рода и имеющему вид

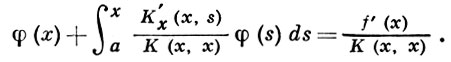
Если К(х, х) = 0 по крайней мере в одной точке, решение В. у. I рода требует более сложного исследования. Если же К(х, x) ≡ 0, то (при нек-рых условиях) операцию дифференцирования можно повторить. В случае, когда дифференцирование невозможно или не приводит к В. у. II рода, можно, вообще говоря, указать только тривиальный критерий разрешимости. Именно, В. у. (1) разрешимо тогда и только тогда, когда f принадлежит области значений интегрального оператора Вольтерра левой части. Решение В. у. (1) в этом случае может быть получено, напр., при помощи регуляризующего алгоритма (см. Регуляризация).

Для практич. приложений В. у. II рода весьма важно уметь хотя бы приближенно вычислить его решение, напр., при помощи последовательных приближений. Однако обычно более удобны методы другого типа, один из к-рых заключается в следующем. Пусть f и К -непрерывные функции. Отрезок [а, b] разбивается точками деления х_i на N равных частей, причем х₀ = а, x_N = b. Для того чтобы найти приближенно φ(х_i), интеграл по отрезку заменяется квадратурной суммой, напр. при помощи формулы прямоугольников с узлами х₀, ..., x_i-1:

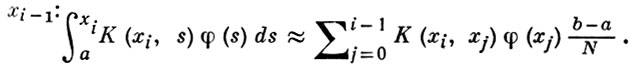
Для получения φ(x_i) используется рекуррентное соотношение:

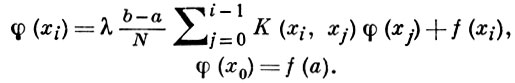
(4)

Значения приближенного решения в точках из [а, b], лежащих между точками деления, могут быть найдены, напр., при помощи соотношения:

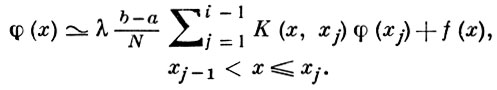
(5)

Это приближенное решение при N → -∞ сходится равномерно к точному решению В. у. II рода.

Возможны многочисленные модификации приведенного метода.

Все сказанное выше справедливо также для В. у., у к-рых ядро К(х, s) есть матрица размера r × r, а φ и f суть r-мерные вектор-функции.

Уравнением Вольтерра, или обобщенным уравнением Вольтерра, наз. также более общее интегральное уравнение вида:

φ(P) - λ ∫_D(P) K(P, Q) φ(Q) dQ = f(P), (6)

если последовательные приближения вида (3) сходятся в том или ином смысле (напр., равномерно или в среднем) на области определения функций φ и f при λ ≠ ∞. Здесь Р и О - точки n-мерного евклидова пространства, D(P) - область интегрирования, вообще говоря, зависящая от точки Р, и D(P) ⊆ D при любом Р. Примером может служить уравнение:

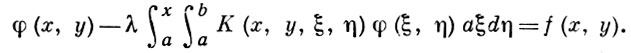
Если функция К(х, у, ξ, η) суммируема с квадратом при а ≤ х ≤ b, a ≤ y ≤ b, a ≤ ξ ≤ b, a ≤ η ≤ b, a f(x, у) суммируема с квадратом при a ≤ x ≤ b, a ≤ y ≤ b, то последовательность (3) сходится в среднем квадратическом при λ ≠ ∞. Обобщенное В. у. I рода обычно не удается свести к В. у. II рода, хотя такие случаи возможны.

Дальнейшим обобщением В. у. вида (2) и (6) служит линейное операторное уравнение:

φ - λAφ = f, (7)

где φ и f - элементы банахова пространства Е, λ -комплексный параметр, А - линейный вполне непрерывный оператор. Это уравнение наз. операторным уравнением Вольтерра, а оператор А - оператором Вольтерра, или абстрактным оператором Вольтерра, если оператор (I - λА) обратим в Е при любом λ ≠ ∞. В этом случае последовательность вида: φ₀ ∈ E - произвольное, φ_n+1 = λAφ_n + f, сходится по норме пространства Е к решению уравнения (7). В современной теории операторов Вольтерра и В. у. установлены глубокие связи между абстрактным и обычным интегральным операторами Вольтерра.

Нелинейными уравнениями Вольтерра наз. иногда В. у., в к-рых произведение К(х, s) φ(s) заменено нек-рой нелинейной (относительно φ(s)) функцией К(х, s, φ(s)). Уравнения такого типа часто встречаются в теоретических и прикладных исследованиях. Так, задача Коши для обыкновенного дифференциального уравнения может быть легко сведена к задаче решения нелинейного В. у. Применение теории потенциала к краевым задачам для уравнений параболич. типа сводит эти краевые задачи к обобщенному В. у. Для нелинейных В. у. при тех или иных предположениях относительно К(х, s, φ(s)) может быть доказана сходимость последовательных приближений вида (3) на отрезке [а, а + Δа], где Δа достаточно мало. Для приближенного решения нелинейных В. у. применяется рекуррентное соотношение (4); нужно только заменить К(х_i, x_j) φ(x_j) на К(х_i, x_j, φ(x_j)). В случае, когда К(х, s, φ(s)) не зависит от х, этот метод совпадает с методом Эйлера.

Лит.: [1] Volterra V., «Rend. Accad. Lincei», 1896, t 5, p. 177-185, 289-300; [2] eго же, «Аnn. di math.», 1897, (2), t. 25, p. 139-187; [3] Смирнов В. И., Курс высшей математики, т. 4, 5 изд., М., 1958; [4] Владимиров В. С., Уравнения математической физики, М., 1967; [5] Петровский И. Г., Лекции по теории интегральных уравнений, 3 изд., М., 1965; [6] Тихонов А. Н., «Бюллетень Моск. ун-та» (А), 1938, т. 1, в. 8, с. 1-25.

А. Б. Бакушинский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.