ВОДОРОДОПОДОБНЫЙ АТОМ

ВОДОРОДОПОДОБНЫЙ АТОМ - квантовомеханическая система, состоящая из ядра массы М с зарядом +Z_e и одного электрона массы m с зарядом -е, взаимодействующих по закону Кулона, т. е. притягивающихся друг к другу с силой, обратно пропорциональной квадрату расстояния между ядром и электроном. В частном случае при Z = 1, когда ядром является протон, В. а. - обычный атом водорода. К В. а. можно отнести мезоатом (μ-мезон в кулоновском поле ядра) и позитроний (система, состоящая из электрона и позитрона). Задача о В. а.- точно решаемый пример общей задачи двух тел в механике (как в классической, так и в квантовой) и является квантовомеханич. аналогом классич. проблемы Кеплера в теории движения двух масс под действием сил всемирного тяготения. После выделения движения центра инерции квантовомеханич. задача о В. а. сводится в нерелятивистском приближении к решению Шрёдингера уравнения для частицы с приведенной массой m₀ = mМ/(m + М), движущейся в поле центральных сил с кулоновским потенциалом:

(*)

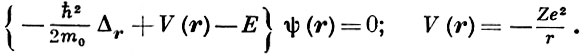
Удовлетворяющие физич. условиям ограниченности волновых функций ψ(r) решения (*) существуют: а) при E_n = -Z²e⁴m/2ħ²n² и целом n ὅ 1 (дискретный спектр энергий E); б) при любом E > 0 (непрерывный спектр энергий). Решения, принадлежащие дискретному спектру, соответствуют стационарным связанным состояниям электрона в В. а. и обладают так наз. «случайным вырождением», т. е. состояния с различными квантованными значениями орбитального момента l = 0, 1, 2, ..., n - 1, а не только его проекции m_l(-l ≤ m_l ≤ l; m_l - целое) на нек-рую ось (обычное вырождение), обладают одинаковой энергией Е_n. «Случайное вырождение» является следствием того, что в частном случае кулоновского потенциала уравнение Шрёдингера (*) инвариантно не только относительно группы ортогональных преобразований О (3), что справедливо для любого потенциала центральных сил, но и относительно преобразований более широкой группы О (4). Решения непрерывного спектра соответствуют ионизованным состояниям В. а., т. е. несвязанным состояниям электрона, и вырождены с бесконечной кратностью - возможны состояния со всеми целыми значениями l ὅ 0 и всеми целыми значениями m_l при данном l, -l ≤ m_l ≤ l.

Релятивистские эффекты в В. а.: зависимость массы от скорости и спиновые свойства электрона и ядра, можно учесть при использовании вместо уравнения Шрёдингера (*) релятивистского Дирака уравнения для электрона в поле кулоновского потенциала ядра.

Учет релятивистских эффектов и спина электрона дает поправки к Е_n, к-рые зависят от l и полного момента j электрона, определяемого через l и спин электрона, и тем самым снимает случайное вырождение уровней энергии В. а. и определяет так наз. тонкую структуру дискретного спектра уровней энергии В. а. Учет спина ядра и связанного с ним магнитного момента, взаимодействующего с движущимся вокруг ядра электроном, а также учет конечных размеров ядра и возможного квадрупольного момента и других высших мультипольных моментов ядра дает дополнительные поправки к Е_n, определяющие так наз. сверхтонкую структуру уровней энергии В. а.

Лит.: [1] Соколов А. А., Лоскутов Ю. М., Тернов И. М., Квантовая механика, 2 изд., М., 1965.

В. Д. Кукин.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.