ВНУТРЕННЕЕ ОТОБРАЖЕНИЕ

ВНУТРЕННЕЕ ОТОБРАЖЕНИЕ - отображение f : X → Y топологич. пространства X в топологич. пространство Y такое, что образ любого открытого в X множества U открыт в Y, а прообраз f^-1(у) любой точки y ∈ Y вполне несвязен (т. е. не содержит связных компонент, отличных от точки).

Пусть F отображает нек-рую риманову поверхность R на сферу S², тогда гомеоморфизм Т : M → R ориентированной поверхности М индуцирует отображение

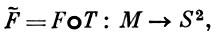
топологически эквивалентное F. Для топологич. эквивалентности аналитич. функции F и нек-рого отображения F̃ необходимо и достаточно, чтобы F было внутренним отображением (тогда существует гомеоморфизм T такой,что F̃ = F ○ T) (теорема Стоилова).

Локальная структура В. о. F̃ : M → ℝ² описывается следующим образом: для любой точки а ∈ М существуют окрестность U(а) и гомеоморфизмы T₁ : B → U(a) единичного круга B = {z ∈ ∨², |z| < 1} на U(а) и Т₂ : F̃(U(a)) → B такие, что T₂ ○ F̃ ○ T₁ = zⁿ.

Лит.: [1] Стоилов С., Лекции о топологических принципах теории аналитических функций, пер. с франц., М., 1964.

В. А. Зорич.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.