ВНЕШНЯЯ МЕРА

ВНЕШНЯЯ МЕРА - неотрицательная функция множества, обозначаемая μ*, заданная на счетно аддитивном классе множеств, содержащем вместе с множеством любое его подмножество и обладающая свойствами; монотонности, т. е.

μ*(Х)≤ μ*(Y), если X ͂ Y;

счетной полуаддитивности, т. е.

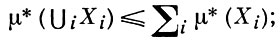
μ*(∅) = 0, где ∅ - пустое множество.

В. м., заданная на всех подмножествах метрич. пространства, наз. В. м. в смысле Каратеодори, или метрической В. м., если

μ*(Х ∪ Y) = μ*(X) + μ*(Y),

как только ρ(X, Y) > 0, где ρ(X, Y) - расстояние между множествами X и Y. По данной В. м. может быть выделен класс измеримых множеств, на к-рых μ* становится мерой.

В. м., в частности, возникают при построении продолжения меры с кольца R на порожденное им σ-кольцо.

В классич. теории Лебега меры (см. [1]) внешняя мера множества определяется как нижняя грань мер открытых множеств, содержащих данное множество, а внутренняя мера множества - как верхняя грань мер замкнутых множеств, содержащихся в заданном множестве.

Лит.: [1] Натансон И. П., Теория функций вещественной переменной, 2 изд., М., 1957; [2] Сакс С., Теория интеграла, пер. с англ., М., 1949; [3] Халмош П., Теория меры, пер. с англ., М., 1953.

В. А. Скворцов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.