ВЛОЖЕНИЯ ТЕОРЕМЫ

ВЛОЖЕНИЯ ТЕОРЕМЫ - теоремы, относящиеся к циклу вопросов, посвященных изучению неравенств между нормами одной и той же функции, принадлежащей к разным классам (нормированным пространствам). Обычно речь идет о двух классах и ₁, где есть часть ( ⊂ ₁), и при этом выполняется неравенство 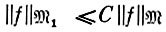для всех f ∈ , где С - константа, не зависящая от f, а ||⋅||, ||⋅||₁ - нормы соответственно в , ₁. При указанных условиях говорят, что имеет место вложение в ₁ или, что вкладывается в ₁, и пишут → ₁. Исследования, связанные с В. т., составляют раздел теории функций, но главные направления в них развиваются под влиянием краевых задач математической физики, в частности прямых вариационных методов. В связи с этим в течение последних трех десятилетий создана стройная теория вложений классов дифференцируемых функций многих переменных.

К числу задач, решаемых В. т., относятся, напр., следующие. Пусть известно, что функция f имеет частные производные порядка l, вообще говоря, обобщенные (см. Обобщенная производная), интегрируемые в р-й степени на данной области Ω n-мерного пространства R_n. Спрашивается: 1) какое гарантированное число непрерывных производных имеет эта функция на Ω? 2) если область Ω имеет достаточно гладкую границу Г, то можно ли в том или ином смысле определить след φ(х) функции f в точках х ∈ Г, т. е. предельные значения f(u), когда u приближается к x, и какими гарантированными дифференциальными свойствами обладает этот след? При этом часто надо знать эти свойства настолько точно, чтобы наличие таковых у функции φ, заданной на Г, влекло возможность продолжения φ с Г на Ω так, чтобы продолженная функция имела на Ω обобщенные производные порядка l, интегрируемые в р-й степени. Из фактов, приводимых ниже, будет видно, что указанные пределы (понимаемые в смысле сходимости почти всюду) определения следа φ функции f и продолжения φ могут сопровождаться неравенствами между нормами f на Ω и Г, к-рые и применяются в теории краевых задач.

Многомерная теория вложений классов дифференцируемых функций возникла в 30-х гг. 20 в. в работах С. Л. Соболева в связи с решением задач математич. физики. Ему принадлежат основные В. т. для классов W^l_p(Ω) (Соболева пространств), играющих важную роль в анализе. Функция f(x) = f(x₁, ..., x_n) принадлежит W^l_p(Ω), 1 ≤ р ≤ ∞, l = 0, 1, ..., если она определена на Ω и для нее конечна норма

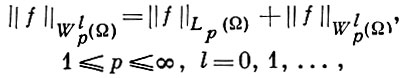
(1)

где

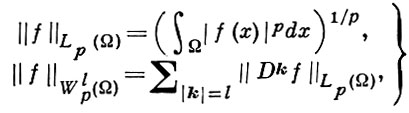
(2)

и сумма распространена на всевозможные (обобщенные по Соболеву) частные производные

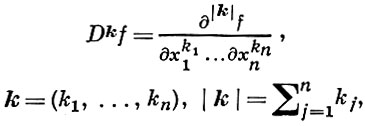
(3)

порядка |k| = 1.

Основная теорема С. Л. Соболева (с дополнениями В. И. Кондрашова и В. П. Ильина) для случая Ω = R_n:

при условиях 1 ≤ m ≤ n, 1 < р < q < ∞, 0 ≤ k = l - 1/p + m/q справедливо вложение

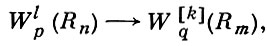
(4)

где [k] - целая часть k.

При m < n это означает, что функция f ∈ W^l_p(R_n) имеет след (см. ниже) на любой координатной гиперплоскости R_m размерности m,

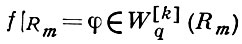
и

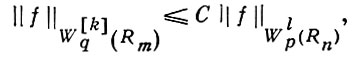
где С не зависит от f (см. [6], [7]).

Функция f, заданная на R_n, имеет след на R_m, где R_m есть m-мерное (координатное) подпространство точек x = (x₁, ..., x_m, x⁰_m+1, ..., x⁰_n) с фиксированными x⁰_m+1, ..., x⁰_n, если f можно видоизменить на нек-ром множестве n-мерной меры нуль так, чтобы для видоизмененной функции, к-рая снова обозначается через f, имело место

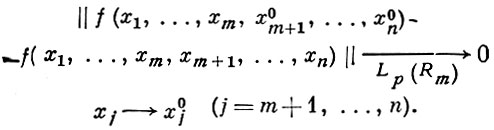
(5)

Если есть множество функций f, заданных на R_n, то задача описания свойств следов этих функций на подпространство R_m(1 ≤ m < n) наз. проблемой следов для класса .

Теорема (4) является окончательной в терминах классов W^l_p(Ω). Дальнейшее ее улучшение возможно лишь путем введения новых классов.

В одномерном случае n = m = 1, где проблема следов не возникает, теорема (4) принадлежит Г. Харди и Дж. Литлвуду (G. Hardy, J. Littlewood).

Следующим этапом в развитии этой теории являются теоремы вложения С. М. Никольского для обобщенных гёльдеровых классов (см. Гёльдерово пространство) (H-классов). Эти классы образуют шкалу с непрерывно меняющимися параметрами, характеризующими гладкость функций. Они анизотропны в том смысле, что принадлежащие к ним функции обладают, вообще говоря, разными дифференциальными свойствами по разным направлениям. Пусть Ω_η есть множество точек х ∈ Ω, удаленных от границы Ω больше чем на η > 0, и пусть r = (r₁, ..., r_n) - положительный вектор (r_j > 0; j = 1, ..., n), r_j = r*_j + α_j, r*_j - целое и 0 < α_j ≤ 1.

Функция принадлежит классу f ∈ H^r_p(Ω), 1 ≤ р ≤ ∞, если f ∈ L_p(Ω) и для любого j = 1, ..., m существует обобщенная частная производная

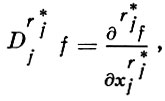
(6)

удовлетворяющая неравенству

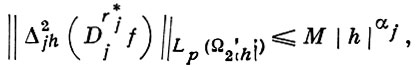
(7)

где Δ²_jh - вторая разность функции по переменной x_j с шагом h и M - константа, не зависящая от h.

Класс H^r_p(Ω) образует банахово пространство, если ввести норму

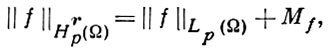
где М_f - наименьшая константа М, при к-рой выполняются неравенства (7). Для r₁ = ... = r_n = r соответствующий (изотропный) класс обозначается через H^r_p. При целом l класс H^l_p близок к классу Соболева W^l_p с точностью до ε > 0 в том смысле, что

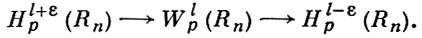
(8)

Справедливы теоремы вложения (С. М. Никольский)

(9)

где 1 ≤ р ≤ q ≤ ∞, 1 ≤ m ≤ n, ρ = (ρ₁, ..., ρ_m),

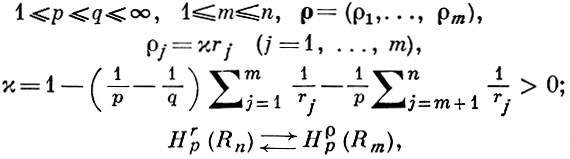
(10)

где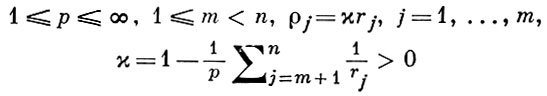

(см. [5]).

Теорема (9) является анизотропным аналогом теоремы (4), но имеет то преимущество, что верхние (векторные) индексы r, ρ фигурирующих в ней классов могут изменяться непрерывно. Кроме того, она полностью охватывает случаи р = 1, ∞. Однако при א = 0 она, в отличие от (4), неверна. В одном случае (n = m = 1) при r и ρ не целых она доказана Г. Харди и Дж. Литлвудом.

Частный случай теоремы (9) при р = q записан еще раз в виде вложения (10) с верхней стрелкой. Оно гласит: функция f ∈ H^r_p(R_n) имеет след f|_Rm = φ на R_m и при этом

(11)

где С не зависит от f. Но справедливо и обратное утверждение, выражаемое нижней стрелкой, к-рое надо понимать в следующем смысле: каждая определенная на R_m функция φ ∈ H^ρ_p(R_m) может быть продолжена на все пространство R_n так, что полученная функция f(х) (со следом на R_m, равным φ) принадлежит к H^r_p(R_n) и выполняется неравенство (обратное к (11)):

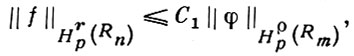
где С₁ не зависит от φ.

Взаимно обратные вложения (10) полностью решают проблему следов для H-классов и при этом в терминах H-классов.

Теорема (9) носит транзитивный характер, заключающийся в том, что переход

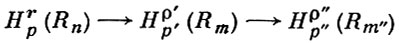
(12)

от первого класса в цепи (12) ко второму, а затем от второго к третьему, где параметры ρ', ρ'' вычисляются по указанным в (9) формулам, может быть заменен одним переходом от первого класса к третьему при непосредственном вычислении ρ'' по тем же формулам.

В дальнейшем (см. далее [14]) была решена проблема следов для W-классов, вообще анизотропных. Это привело к введению нового семейства классов дифференцируемых функций многих переменных B^r_pθ(R_n), зависящих от векторного параметра r и двух скалярных параметров р, θ, удовлетворяющих неравенствам 1 ≤ р, θ ≤ ∞. Во всей полноте это семейство определил О. В. Бесов, изучивший также его основные свойства.

Функция f принадлежит классу W^l_p(Ω), где l = (l₁, ..., l_n) - целый вектор, если для нее имеет смысл конечная норма

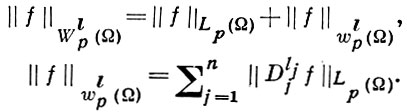
(13)

Функция f принадлежит классу B^r_pθ(Ω), где r = (r₁, ..., r_n) - произвольный, не обязательно целый вектор, 1 ≤ р ≤ ∞, 1 ≤ θ < ∞, r_j > 0, если для нее конечна норма

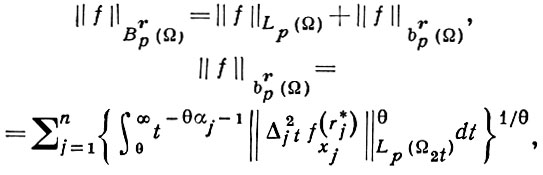
где числа r*_j и α_j определены выше.

Естественно считать, что класс B^r_pθ при 0=∞ совпадает с классом H^r_p(B^r_p∞ = H^r_p). Обычно пишут еще B^r_pθ вместо B^r_pθ, когда r₁ = ... = r_n = r и B^r_p = B^r_pp, B^r_p = B^r_pp. Для любых указанных р, θ, r классы ^r_pθ суть банаховы пространства.

Теоремы вложения (9), (10) верны, если в них заменить H на В. Имеют место также взаимно обратные вложения

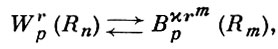
(14)

где r - целое, 1 < р < ∞, r^M = (r₁, ..., r_m, 0, ..., 0), 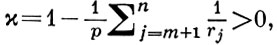полностью решающие проблему следов для W-классов, что не мешает выполняться взаимно обратным вложениям, выраженным полностью на языке B-классов:

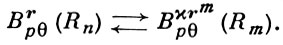
(15)

Классы B^r₂ соответствующие значениям параметров p = θ = 2, принято еще обозначать через W^r₂(B^r₂ = W^r₂). При р = 2 вложения (14) записываются еще и так

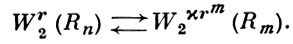
(16)

Естественными продолжениями W-классов являются классы, в определении к-рых фигурирует понятие дробной производной по Лиувиллю (см. Дробное интегрирование и дифференцирование).

Употребляя терминологию обобщенных функций, можно задать основной класс Λ функций так, что построенный над ним класс Λ' обобщенных функций будет обладать следующими свойствами: 1) L_p(R_n) ⊂ Λ' при любом конечном р ≥ 0; 2) при любом l > 0, не обязательно целом, имеет смысл операция

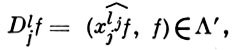
(17)

где ψ̃, ψ̂ означают соответственно прямое и обратное Фурье преобразование ψ ∈ Λ'; 3) если l - целое и функция f ∈ L_p(R_n) имеет обобщенную по Соболеву производную D^l_jf ∈ L_p(R_n), то для нее имеет место равенство (17).

При дробных l на бесконечно дифференцируемых финитных функциях операция (17) совпадает с операцией дробного дифференцирования по Лиувиллю. Естественно называть D^l_jf при нецелом l дробной производной от f порядка l по х_j.

Если теперь задан произвольный вектор l = (l₁, ..., l_n), то можно ввести пространство L^l_p(R_n), 1 ≤ р < ∞, совпадающее с W^l_p(R_n) при целых l, заменив в (13) W на L.

Если l = l₁ = ... = l_n, то положим L^l_p = L^l_p. Семейство классов L^l_p(R_n), l > 0, 1 ≤ р < ∞, может рассматриваться как естественное расширение семейства W^l_p(R_n) на дробное l, «естественное» потому, что с точки зрения интересующего нас круга идей классы L^l_p обладают «всеми достоинствами и недостатками классов W^l_p». Если в формуле (4) (где [k] можно заменить на k), или (8) (где l может быть дробным), или в (14), (16) (где r может быть дробным) заменить W на L, то они останутся верными. Верной также останется формула (9), если в ней заменить Н на L даже при более широком условии א ≥ 0, однако в предположении, что 1 < р < q < ∞.

В дальнейшем продолжается применение аппарата обобщенных функций, но теперь уже составляющих пространство S'. Для любого действительного числа ρ имеет смысл операция (Бесселя-Макдональда):

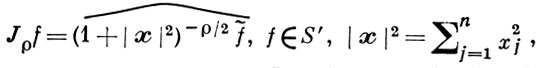
обладающая свойствами: J₀f = f, J_r+ρ = J_rJ_ρ, J_-2l = ((1-Δ)', l = 0, 1, ..., где 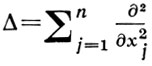- оператор Лапласа.

Изотропный класс L^ρ_p = L^ρ_p(R_n), 1 < р < ∞, может быть определен еще как совокупность функций f, представимых в виде f = J_ρφ, где функции φ пробегают пространство L_p = L_p(R_n) (L^ρ_p = J_ρ(L_p)), при этом, с точностью до эквивалентности,

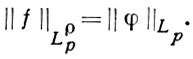
Это определение класса L^ρ_p годится и для отрицательных ρ, но в этом случае L^ρ_p есть совокупность, вообще говоря, обобщенных функций (L^ρ_p ⊂ S'). В частности, L⁰_p = L_p.

Операция J_ρ может служить средством и для определения классов В^r_pθ(В_p∞ = Н^r_p). Именно, будем называть обобщенную функцию f регулярной в смысле L_p или принадлежащей к S'_p, если найдется такое ρ > 0, что J_ρ ∈ L_p. Всякую функцию f ∈ В^r_pθ = B^r_pθ(R_n), 1 ≤ ρ, θ ≤ ∞, B^r_p∞ = H^r_p, можно определить как регулярную в смысле L_p функцию, представимую рядом

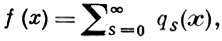
слабо сходящимся к f (в смысле S'), где q₀ имеет спектр (носитель q̃₀) в Δ₀, a q_s при s ≥ 1 имеет спектр в Δ_s+1\Δ_s-1 и

Δ_s = {x; |x_j| ≤ 2^s; j = 1, ..., n},

и при этом

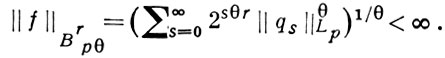
В частности,

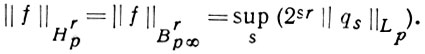
Это определение класса B^r_pθ автоматически распространяется на случай r ≤ 0, и тогда функции f, входящие в эти классы, будут, вообще говоря, обобщенными (f ∈ S'). При этом J_r(B⁰_p) = B^r_p, -∞ < r < ∞.

Существуют и другие эквивалентные определения отрицательных классов В^r_pθ, основанные на принципе интерполяции функциональных пространств. Приведенное определение носит конструктивный характер -каждый заданный параметрами r, р, θ класс определяется независимо, при этом можно конструктивно определить линейные операции, при помощи к-рых по данной функции f ∈ S'_p определяется функция q_s (экспоненциального типа 2^s+1 при s ≥ 1 и типа 1 при s = 0).

Справедлива теорема вложения:

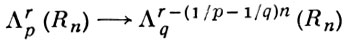
типа теоремы (4), но с n = m, верная при любом действительном r для Λ = L, 1 < р < q < ∞ или для Λ = В, 1 ≤ p < q < ∞, 1 ≤ θ < ∞ или для Λ = Н, 1 ≤ р < q ≤ ∞.

С другой стороны, при r - (n - m)/р = 0 произвольная функция f ∈ Λ^r_p(R_n), вообще говоря, не имеет следа на R_m(m < n), если не налагать на нее дополнительных условий.

Выше были сформулированы В. т. для классов функций, определенных на всем n-мерном пространстве R_n (см. [5]). Но для приложений важно иметь подобные теоремы для возможно общих областей Ω ⊂ R_n. В настоящее время выяснена геометрия, структура областей Ω, для к-рых верны указанные теоремы вложения для W-, В- и H-классов, где надо заменить R_n, R_m соответственно на Ω, R_m ∩ Ω. Для изотропных классов W^r_p(Ω), B^r_pθ(Ω) область Ω должна удовлетворять условию конуса или, что равносильно, граница ее должна удовлетворять локально условию Липшица. Для анизотропных же классов W^r_p(Ω), B^r_p(Ω) область Ω должна удовлетворять условию r-рога или изогнутого конуса (конуса условие) и это условие является в известном смысле необходимым (см. [2]).

Для приложений важна еще проблема о следах на m-мерных многообразиях S_m.

Для изотропных классов W, Н, В эта проблема решена полностью (см. [2], [16]), если S_m достаточно много раз дифференцируемо при r = r₁ = ... = r_n, в (14), (15) u (16) можно заменить R_m на S_m, а в (19), кроме того, можно заменить Н на В. В случае кусочно гладких S_m этот вопрос тоже в ряде случаев решен до конца ([16], [22]), условия, решающие проблему, выражаются, с одной стороны, указанными выше взаимно обратными вложениями на отдельных гладких кусках S_m, а с другой- специальными дополнительными условиями на поведение функций соответствующих классов на стыках этих гладких кусков. Существенно продвинута также проблема следов для анизотропных классов ([9], [21]). Здесь возникают особые затруднения характеристики следа в точках S_m, касательные плоскости к к-рым параллельны осям координат.

Остановимся еще на одной задаче. Пусть функция

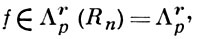
где Λ^r_p означает один из рассмотренных выше классов. Спрашивается, какие она имеет частные смешанные производные D^kf и каковы их свойства? Положительный ответ на этот вопрос зависит от величины

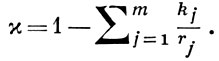
Именно, если f ∈ Λ^r_p то существует частная производная D^kf, принадлежащая к пространству Λ^אr_p при условии, что א > 0. В случае же пространств L^r_p это условие можно расширить, считая א ≥ 0 (см. [5]).

Приведем еще характерную теорему, к-рую естественно назвать теоремой об ослабленной компактности и к-рая имеет применение в теории прямых методов вариационного исчисления.

Из бесконечного множества функций f, удовлетворяющих неравенству

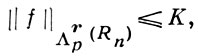
где K - заданная константа, а Λ - один из рассмотренных выше классов, можно выделить последовательность {f_m} функций и указать такую функцию f₀ с нормой

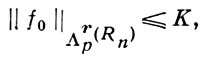
что какова бы ни была ограниченная область G ⊂ R_n и вектор ε > 0

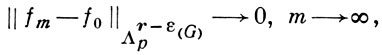
(см. [5]). В этой формулировке R_n может быть заменено на область Ω, если она имеет достаточно хорошую границу. Выше были рассмотрены только характерные классы функций и связанные с ними теоремы вложения, наиболее часто встреяающиеся в приложениях. В современных исследованиях большое внимание [2] уделяется классам более общим, где роль исходных частных производных D^kf, D^p_jf играют более или менее произвольные дифференциальные операторы.

Изучаются еще так наз. весовые классы, характерным примером к-рых является класс W^r_pα(Ω), определяемый следующим образом. Пусть ρ(x) есть расстояние от точки x до границы Г области Ω ⊂ R_n. Функция f принадлежит к W^r_pα(Ω), r > 0, 1 ≤ р < ∞, если для нее конечна норма (см. [4], [12])

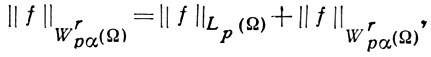
где

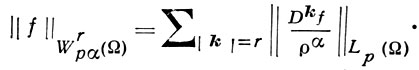
Приведем только один результат. Пусть Г_m - достаточно гладкая граница m измерений; тогда

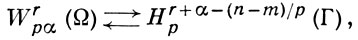
если r + α - (n - m)/р > 0, α < (n - m)/р, 1 < р < ∞.

Пример. Использование В. т. полностью решает вопрос об условиях на граничную функцию, при к-рых применим Дирихле принцип. Именно, понимая частные производные в обобщенном смысле и считая для простоты, что поверхность Г (граница трехмерной области) ограничена и дважды дифференцируема, задаем на Ω функцию f₀ ∈ W¹₂(Ω). Для нее Дирихле интеграл D(f₀) < ∞ и, кроме того, по В. т.

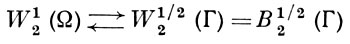
f₀ имеет след на Г (факт существования следа у f₀ устанавливался при помощи более грубых В. т.). Обозначив через класс функций f ∈ W¹₂(Ω), имеющих тот же след на Г, что и f₀, f|_Г = f₀|_Г = φ, можно сформулировать принцип Дирихле следующим образом: минимум D(f) среди функций f ∈ достигается для единственной функции и к тому же гармонической на Ω. Из приведенной В. т. следует, что принцип Дирихле применим тогда и только тогда, когда класс не пуст, т. е. когда граничная функция φ ∈ B^1/2₂(Г).

При обосновании принципа Дирихле сначала доказывается существование и единственность функции u ∈ , а также тот факт, что u есть обобщенное решение задачи Дирихле, а затем при помощи специального метода последовательно устанавливается, что обобщенное решение принадлежит классам W^l₂(ω), где l = 2, 3,..., а ω ∈ Ω - произвольный замкнутый шар. В частности, из того факта, что u ∈ W⁴₂(ω), на основании В. т.

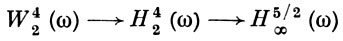
(см. [2] и [5]) при n = m = 3, р = 2, q = ∞, r₁ = r₂ = r₃ = 4) заключаем, что функцию u можно видоизменить на множестве трехмерной меры нуль так, чтобы полученная функция была дважды непрерывно дифференцируема на Ω. После этого легко доказывается, что u - гармоническая.

Приведенный пример может быть значительно обобщен на нек-рые функционалы, в к-рые входят частные производные разных порядков, возведенные в степень, вообще не равную 2 (р ≠ 2), и тогда появляется необходимость применения В. т. для более общих классов, вообще говоря, анизотропных.

Лит.: [1] Сб. дифференциальные уравнения с частными производными, М., 1970, с. 38-63; [2] Бесов О. В., Ильин В. П., Никольский С. М., Интегральные представления функций и теоремы вложения, М., 1974; [3] Буренков В. И., Теоремы вложения и продолжения для классов дифференцируемых функций многих переменных во всем пространстве, в кн.: Итоги науки. Математический анализ. 1965, М., 1966; [4] Никольский С. М., «Успехи матем. наук», 1961, т. 16, в. 5, с. 63-114; [5] его же, Приближение функций многих переменных и теоремы вложения, М., 1969; [6] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Л., 1950: [7] его же, Введение в теорию кубатурных формул, М., 1974; [8] Бесов О. В., «Труды Матем. ин-та АН СССР», 1961, т. 60, с. 42-81; [9] Бугров Я. С., «Сиб. матем. ж.», 1964, т. 5, № 5, с. 1007-26; [10] Ильин В. П., «Докл. АН СССР», 1954, т. 96, № 5, с. 905-8; [11] Кондратов В. И., там же, 1945, т. 48, с. 563-6; [12] Кудрявцев Л. Д., «Труды Матем. ин-та АН СССР», 1959, т. 55, с. 1-182; [13] Лизоркин П. И., «Докл. АН СССР», 1960, т. 132, № 3, с. 514-17; [14] его же, «Матем. сб.», 1963, т. 60, в. 3, с. 325-53; [15] Никольский С. М., «Труды Матем. ин-та АН СССР», 1951, т. 38, с. 244-78; [16] его же, «Матем. сб.», 1953, т. 33, в. 2, с. 261-326; 1957, т. 43, в. 7, с. 127-44; [17] Соболев С. Л., «Докл. АН СССР», 1935, т. 3, № 7, с. 291-4; [18] его же, «Матем. сб.», 1936, т. 1, в. 1, с. 39-72; 1938, т. 4, в. 3, с. 471-97; [19] Слободецкий Л. Н., «Докл. АН СССР», 1958, т. 118, в. 2, с. 243-6; [20] Успенский С. В., «Труды Матем. ин-та АН СССР», 1961, т. 60, с. 282-303; [21] его же, «Докл. АН СССР», 1965, т. 164, № 4, с. 750-2; [22] Яковлев Г. Н., «Труды Матем. ин-та АН СССР», 1961, т. 60, с. 325-49; [23] Gagliardo Е., «Rend Semin. matem. in-ta di Padova», 1957, t. 27, p. 284-305; [24] Hardy G. H., Lilttlewood J. E., «Math. Z.», 1928, Bd 28, №4, S. 612-34; [25] Lions J. L., Magehes E., Problemes aux limites non homogénes et applications, P., 1968, v. 1-2.

С. M. Никольский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.