ВКЛЮЧЕНИЯ И ИСКЛЮЧЕНИЯ ПРИНЦИП

ВКЛЮЧЕНИЯ И ИСКЛЮЧЕНИЯ ПРИНЦИП - метод подсчета числа N (а'₁а'₂...а'_r) объектов, не обладающих ни одним из данных свойств а₁, а₂, ..., а_r, по следующей формуле:

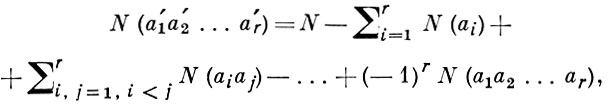
(1)

где а'_i означает отсутствие свойства а_i, N - число всех объектов, N(а_i) - число объектов, обладающих свойством а_i, N(а_iа_j) - число объектов, обладающих одновременно свойствами а_i и a_j, и т. д. (см., напр., [3]). Из В. и и. п. вытекает формула для подсчета числа объектов, обладающих точно m свойствами из а₁, а₂, ..., a_r, m = 0, 1, ..., r:

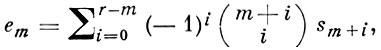
(2)

где s₀ = N, s_k = ∑N(a_i1a_i2...a_ik) причем здесь суммирование производится по всем fe-наборам (i₁, i₂, ..., i_k) таким, что i₁ ≠ i₂ ≠ i_k, k = 1, ..., r, т. е. s₁ = ∑_iN(a_i) s₂ = ∑_i,j,i≠jN(a_ia_j), ..., s_r = N (a₁a₂ ... a_r).

Иногда метод подсчета е_m по формуле (2) также наз. В. и и. п. Этот принцип находит применение при решении комбинаторных и теоретико-числовых задач (см., напр., [1]). Так, если дано натуральное число а и натуральные числа a₁, а₂, ..., a_N такие, что (а_i, а_j) = 1 при i ≠ j, то число целых чисел к таких, что 0 < k ≤ n и не делящихся на а_i, i = 1, 2, ..., N, равно по (1):

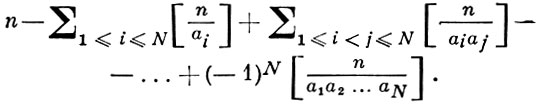
При помощи В. и и. п. решается также задача о беспорядках (см. [2], [3]).

Лит.: [1] Холл М., Комбинаторика, пер. с англ., М., 1970; [2] Райзер Г. Дж., Комбинаторная математика, пер. с англ., М., 1966; [3] Риордан Дж., Введение в комбинаторный анализ, пер. с англ., М., 1963.

С. А. Рукова

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.