ВКБ-МЕТОД

ВКБ-МЕТОД - асимптотический метод Вентцеля-Крамерса-Бриллюэна (и Джефриса) решения обыкновенных дифференциальных уравнений вида

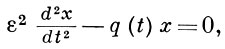
(1)

с малым параметром ε > 0 при старшей производной. Для построения приближенных решений волнового уравнения Шрёдингера в квантовой механике этот метод был введен в 1926 Л. Бриллюэном (L. Brillouin), Г. Вентцелем (G. Wentzel) и X. Крамерсом (Н. Kramers), а также X. Джефрисом (Н. Jeffreys) (подробный историч. очерк и библиографию см. в [5], [6]). Для ВКБ-м. используются и другие названия: «приближение Лиувилля-Грина», «метод фазового интеграла», «квазиклассическое приближение», а также любые комбинации из букв W, K, B (и J).

Пусть I = [a, b], q(t) ∈ ℂ^∞(I) и Re √q(t) ≥ 0 при t ∈ I или q(t) < 0 при t ∈ I. Тогда существуют решения уравнения (1) такие, что при ε → +0 равномерно по t ∈ I

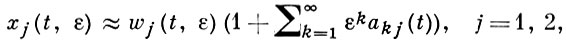
причем

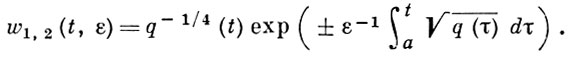
(2)

Главный член асимптотич. разложения (2) обычно наз. ВКБ-приближением.

Пусть I = [0, +∞), предыдущие условия на q(t) выполнены и

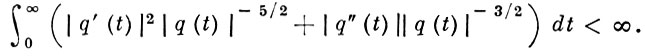
Тогда существуют решения уравнения (1) такие, что x_j(t, ε) = W_j(t, ε)(1 + εφ_j(t, ε)), j = 1, 2, где |φ_j(t, ε)| ≤ С при t ∈ I, 0 ≤ ε ≤ ε₀, если ε₀ > 0 достаточно мало, и φ_j(t, ε) → -0 при f → +∞, ε > 0.

Точка t₀ наз. точкой поворота уравнения (1), если q(t₀) = 0. ВКБ-приближение непригодно в точках поворота. Были получены асимптотич. формулы, справедливые в окрестностях точек поворота (см. [1], [4]). Главный член асимптотики выражается через бесселевы функции.

В ряде задач (задача на собственные значения, задача о рассеянии) для уравнения (1) требуется знать асимптотику решений только на концах интервала, т. е. не нужно находить асимптотику в точках поворота. Если q(t) - аналитич. функция, то можно, вообще говоря, продолжить ВКБ-формулы с одного конца интервала I на другой через комплексную плоскость ℂ(t) (строгое обоснование дано в [2]). Для целых функций q(t) оказывается, что ВКБ-приближение (2) пригодно в нек-рых областях комплексной плоскости ℂ(t), ограниченных линиями Стокса (т. е. линиями уровня 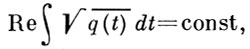, проходящими через точки поворота). Получены асимптотич. формулы для фундаментальной системы решений уравнения (1), пригодные во всей комплексной плоскости, за исключением окрестностей точек поворота (см. [2]).

О ВКБ-приближении для уравнений с частными производными см. [5], [6], [8]-[10].

Лит.: [1] Вазов В., Асимптотические разложения решений обыкновенных дифференциальных уравнений, пер. с англ., М., 1968; [2] Евграфов М. А., Федорюк М. В., «Успехи матем. наук», 1966, т. 21, № 1, с. 3-50; [3] Федорюк М. В., Добавление к книге В. Вазова [1], с. 406-33; [41 Дородницын А. А., «Успехи матем. наук», 1952, т. 7, № 6, с. 3-96; [5] Xединг Дж., Введение в метод фазовых интегралов (Метод ВКБ), пер. с англ., М., 1965; [6] Фрёман Н., Фрёман П. У., ВКБ-приближение, пер. с англ., М., 1967; [7] Ландау Л. Д., Лифшиц Е. М., Квантовая механика, 2 изд., М., 1963; [8] Маслов В. П., Теория возмущений и асимптотические методы, М., 1965; [9] его же, Операторные методы, М., 1973; [10] Маслов В. П., Федорюк М. В., Квазиклассическое приближение для уравнений квантовой механики, М., 1976.

М. В. Федорюк.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.