
ВИХРЬ
ВИХРЬ, ротор, векторного поля а(М) - векторная «вращательная составляющая» этого поля. Если а(М) - поле скоростей частиц движущейся непрерывной среды, то В. равен половине угловой скорости частицы. В. обозначается rot а (иногда - curl а). В декартовых прямоугольных координатах х, у, z В. определяется выражением:
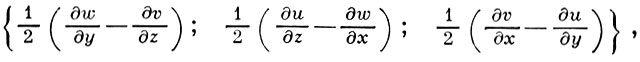
где u(M), v(M), w(M) - компоненты а(M).
Линия в пространстве, в каждой точке к-рой в данный момент времени В. лежит на касательной прямой, наз. вихревой линией. Всякая поверхность, на к-рой расположено семейство вихревых линий, зависящее от одного параметра, наз. вихревой поверхностью. Частным, но весьма важным примером вихревых поверхностей являются вихревые трубки, к-рые образуются вихревыми линиями, выходящими из всех точек какой-нибудь замкнутой кривой. Если эта кривая бесконечно мала, то образующаяся вихревая поверхность наз. вихревой нитью. Вихревые поверхности наз. также вихревыми слоями, считая слой как бы состоящим из геометрич. поверхности с нанесенной на ней обкладкой из вихревых линий. При пересечении вихревого слоя скорости частиц жидкости испытывают тангенциальный разрыв, пропорциональный В. в соответствующей точке.
Основная теорема Гельмгольца в гидродинамике заключается в том, что если объемные силы имеют потенциал, то при течении однородной, идеальной несжимаемой жидкости или баротропного газа частицы среды, расположенные в нек-рый момент времени на вихревой линии, будут и во все последующее время располагаться на вихревой линии. Таким образом, с течением времени сохраняются вихревые поверхности и, в частности, вихревые трубки и нити. Каждая вихревая трубка может быть охарактеризована нек-рым числом, наз. напряженностью трубки, и равным потоку вектора В. через произвольным образом проведенное сечение трубки. Это число не зависит от формы поперечного сечения, так как divrot а = 0. Оно означает, что вихревая трубка может быть либо замкнутой (вихревое кольцо), либо иметь начало и конец на границах жидкости. С течением времени напряженность вихревой трубки в идеальной жидкости не меняется.
Перечисленные свойства вихревых трубок, найденные Г. Гельмгольцем (Н. Helmholtz), получают исключительно простое доказательство с помощью введенного У. Томсоном (W. Thomson) понятия о циркуляции Г скорости v по замкнутому контуру (L):
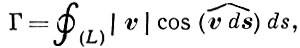
где ds - элемент дуги контура L. Изучение свойств циркуляции скорости приводит к теореме Лагранжа о сохранении с течением времени безвихревого движения.
Основной задачей теории В. является определение поля скоростей движения жидкости по заданному полю векторов В. Если область, занятая жидкостью, безгранична во всех направлениях и если область (D), занятая В., ограничена замкнутой вихревой поверхностью, то поле скоростей находится с помощью вектор-потенциала
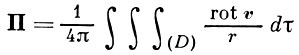
по формуле:
а = rot П.
Если же задача состоит в определении скоростей по вихрям в ограниченном пространстве, то решение весьма сложно вследствие необходимости рассматривать интегральные уравнения с особыми ядрами. Полное решение этой задачи в [6], [7].
Для важного частного случая плоскопараллельных движений:
u = u(х, у), v = v(x, у), w = w(x, у)
две компоненты α, β В. равны нулю, а третья компонента у представляет собой весь В., к-рый в данном случае перпендикулярен к плоскости XOY. В пересечении вихревой нити с плоскостью XOY образуется маленькая площадка, наз. вихревой точкой. При наличии в жидкости нескольких вихревых точек возникает движение самих точек благодаря тем скоростям, какие возбуждают в жидкости эти точки. Уравнения движения вихревых точек имеют вид канонич. уравнений механики.
Лит.: [1] Аппель П., Руководство теоретической (рациональной) механики, пер. с франц., т. 3, М., 1911: [2] Вилля Г., Теория вихрей, пер. с франц., Л.-М., 1936; [3] Lichtenstein L., Grundlagen der Hydromechanik, В., 1929; [4] Милн-Томсон Л. M., Теоретическая гидродинамика, пер. с англ., М., 1964; [5] Ламб Г., Гидродинамика, пер. с англ., М.-Л., 1947; [6] Гюнтер Н. М., «Изв. АН СССР», 6 сер., 1926, т. 20, № 13-14, с. 1323-48; № 15-17, с. 1503-1532; [7] его же, «Ж. Ленингр. Физ.-матем. об-ва», 1926, т. 1, в. 1, с. 12-36.
Л. Н. Сретенский.
Источники:
- Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.
|
ПОИСК:
|
© MATHEMLIB.RU, 2001-2021
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'
При копировании материалов проекта обязательно ставить ссылку на страницу источник:
http://mathemlib.ru/ 'Математическая библиотека'