ВИТТА РАЗЛОЖЕНИЕ

ВИТТА РАЗЛОЖЕНИЕ векторного пространства - разложение пространства в прямую сумму трех подпространств, обладающих определенными свойствами. Точнее, пусть V - векторное пространство над полем k характеристики, отличной от двух, наделенное метрич. структурой с помощью симметрической или знакопеременной билинейной формы f. Прямое разложение

V = N₁ + N₂ + D

наз. В. р. пространства V, если N₁ и N₂ вполне изотропны, a D неизотропно и ортогонально N₁ + N₂ относительно f.В. р. играет важную роль в изучении структуры формы f и в вопросах классификации билинейных форм.

Пусть f - невырожденная билинейная форма и V -конечномерно. Тогда любое максимальное вполне изотропное подпространство в V может быть включено в В. р. пространства V в качестве N₁ (или N₂). Для всякого В. p. dim N₁ = dim N₂ и для любого базиса v₁⁽¹⁾, ..., v_n⁽¹⁾ в N₁ существует такой базис v₁⁽²⁾, ..., v_n⁽²⁾ в N₂, что f(v_i⁽¹⁾, v_j⁽²⁾) = δ_ij (δ_ij - символы Кронекера). Для любых двух В. р.

V = N₁ + N₂ + D = N'₁ + N'₂ + D'

условие dim N_i = dim N'_i, i = 1, 2, необходимо и достаточно для того, чтобы существовал такой метрич. автоморфизм φ пространства V, что

φ(N₁) = N'₁, φ(N₂) = N'₂, φ(D) = D'.

Невырожденная билинейная симметрическая или знакопеременная форма f на V наз. нейтральной, если V конечномерно и обладает В. р. с D = 0. Симметрическая форма в этом случае наз. гиперболической формой, а V - гиперболическим пространством. Ортогональная прямая сумма нейтральных форм нейтральна. Матрица нейтральной формы (в описанном выше базисе v₁⁽¹⁾, ..., v_n⁽¹⁾ , v₁⁽²⁾, ..., v_n⁽²⁾) пространства V = N₁ + N₂) имеет вид

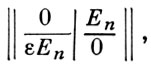
где Е_n - единичная матрица порядка n, а ε = 1 для симметрической формы и -1 для знакопеременной. Нейтральные формы изометричны тогда и только тогда, когда они имеют одинаковый ранг. Класс нейтральных симметрических билинейных форм является нулем (т. е. нейтральным элементом по сложению) в Витта кольце поля k. Нейтральные формы и только они имеют индекс Витта, равный 1/2dim V. Знакопеременная форма на конечномерном пространстве нейтральна.

Если f - невырожденная симметрическая билинейная форма на конечномерном пространстве V и V = N₁ + N₂ + D -В. р., в котором dim N₁ = dim N₂ и равно индексу Витта формы f, то сужение f на D является определенной, или анизотропной, билинейной формой, т. е. такой, что f(v, v) ≠ 0 для любого ненулевого v ∈ D. Эта форма не зависит (с точностью до изометрии) от выбора В. р. на V. В множестве определенных билинейных форм можно ввести

операцию сложения, превращающую его в абелеву группу - группу Витта поля k (см. Витта кольцо).

Пусть v₁⁽ⁱ⁾, ..., v_n⁽ⁱ⁾ - такие базисы в N_i, i = 1, 2, что f(v_i⁽¹⁾), v_j⁽²⁾ = δ_ij, объединяя эти базисы с произвольным базисом в D, получают базис в V, в к-ром матрица формы f имеет вид

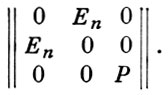
Для симметрических билинейных форм существует ортогональный базис в V, т. е. такой, в к-ром матрица формы диагональна. Если поле k алгебраически замкнуто, то найдется даже ортонормированный базис (базис, в к-ром матрица формы является единичной), поэтому невырожденные симметрические билинейные формы конечного ранга над к изометричны тогда и только тогда, когда они имеют одинаковый ранг. В общем случае классификация таких форм существенно зависит от арифметич. свойств поля k.

Изучение и классификация вырожденных симметрических и знакопеременных билинейных форм сводится k изучению невырожденных форм (сужение формы на подпространство, дополнительное к ядру формы).

Все изложенное допускает обобщение на случай ε-эрмитовых форм над телом, обладающих свойством (Т) (см. Bumma теорема), а также на случай симметрических билинейных форм, ассоциированных с квадратичной формой, без ограничений на характеристику поля.

Лит.: [1] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [2] Ленг С., Алгебра, пер. с англ., М., 1968; [3] Артин Э., Геометрическая алгебра, пер. с англ., М., 1969; [4] Дьедонне Ж., Геометрия классических групп, пер. с франц., М., 1974.

В. Л. Попов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.