ВИТТА КОЛЬЦО

ВИТТА КОЛЬЦО поля k, кольцо типов квадратичных форм над k, - кольцо W(k) классов невырожденных квадратичных форм на конечномерных векторных пространствах над k по следующему отношению эквивалентности: форма f₁ эквивалентна форме f₂(f₁ ~ f₂) тогда и только тогда, когда для некоторых нейтральных квадратичных форм g₁ и g₂ ортогональная прямая сумма форм f₁ и g₁ изометрична ортогональной прямой сумме f₂ и g₂. Операции сложения и умножения в W(k) индуцируются взятием ортогональной прямой суммы и тензорного произведения форм.

Пусть характеристика поля k отлична от 2. Тогда определение эквивалентности форм равносильно следующему: f₁ ~ f₂ тогда и только тогда, когда анизотропные формы f^a₁ и f^a₂, соответствующие f₁ и f₂ (см. Витта разложение), изометричны. Класс эквивалентности формы f наз. ее типом и обозначается [f]. В. к., или кольцо типов квадратичных форм, есть ассоциативно коммутативное кольцо с единицей. Единицей кольца W(k) является тип формы (1). [Здесь через (a₁, ..., a_n) обозначается квадратичная форма f(x₁, ..., x_n) = ∑a_ix²_i.] Нулем служит тип нулевой формы ранга нуль, содержащий также все нейтральные формы. Противоположным к типу [f] является тип [-f].

Аддитивная группа кольца W(k) наз. группой Витта поля k, или группой типов квадратичных форм над k. Типы квадратичных форм вида (а), где а - элемент мультипликативной группы k^× поля k, порождают кольцо W(k). Причем W(k) полностью определяется в этих образующих соотношениями:

(а)(b) = (аb), (а) + (b)= (а + b) + ((а + b)аb), (а)² = 1, (а) + (-а) = 0.

В. к. можно описать как кольцо, изоморфное фактор-кольцу целочисленного группового кольца

ℤ[k^×/(k^×)²]

группы k^×/(k^×)² по идеалу, порожденному элементами

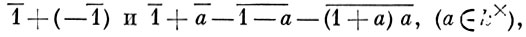
где х̄ - смежный класс элемента х по подгруппе (k^×)².

В ряде случаев В. к. вычисляется явно: напр., если k - квадратично (в частности, алгебраически) замкнутое поле, то W(k) ≃ ℤ/2ℤ; если k - вещественно замкнутое поле, то W(k) ≃ ℤ (изоморфизм осуществляется сопоставлением типу [f] сигнатуры формы f); если k - пифагорово поле (т. е. сумма любых двух квадратов в k является квадратом) и не вещественно, то W(k) ≃ ℤ/2ℤ; если k - конечное поле, то кольцо W(k) изоморфно либо кольцу вычетов ℤ/4ℤ, либо (ℤ/2ℤ)[t]/(t² - 1); если k - полное локальное поле и его поле классов к имеет характеристику, отличную от 2, то

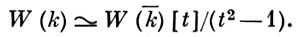
Расширение k' | k поля k определяет гомоморфизм колец Витта φ: W(k) → W(k'), при котором [(a₁, ..., a_n)] → [(a₁, ..., a_n)]. Если расширение конечно и имеет нечетную степень, то φ - мономорфизм, а если, кроме того, оно является Галуа расширением с группой G, то действие группы G продолжается на W(k) и

φ(W(k)) = W(k')^G.

Общие свойства В. к. описываются теоремой Пфистера:

1) для любого поля к периодическая подгруппа W_t(k) группы W(k) 2-примарна;

2) если k - вещественное поле, а k_p - его пифагорово замыкание (т. е. наименьшее пифагорово поле, содержащее k), то точна последовательность

0 → W_t(k) → W(k) → W(k_p)

(при этом, если W_t(k) = 0, то поле k - пифагорово);

3) если {k_α} - семейство всех вещественных замыканий поля k, то точна последовательность

0 → W_t(k) → W(k) → П W(k_α)

в частности,

4) если k - не вещественное поле, то группа W(k) периодическая.

Ряд других результатов относится к мультипликативной теории форм. В частности, пусть m - множество типов квадратичных форм на четномерных пространствах. Тогда m является двусторонним идеалом в W(k) и W(k)/m ≃ ℤ/2ℤ, идеал m содержит все делители нуля кольца W(k), множество нильпотентных элементов кольца W(k) совпадает с множеством элементов конечного порядка идеала m и является радикалом Джекобсона и первичным радикалом кольца W(k). Кольцо W(k) конечно тогда и только тогда, когда поле k не вещественно, а группа k^×/(k^×)² конечна; кольцо W(k) нетерово тогда и только тогда, когда группа k^×/(k^×)² конечна. Если k - не вещественное поле, то m является единственным простым идеалом кольца W(k). Если же k -вещественное поле, то множество простых идеалов кольца W(k) является дизъюнктным объединением идеала m и семейств простых идеалов, соответствующих упорядочениям р поля k:

Р = {[(a₁, ..., a_n)] | ∑sgn_p a_i = 0},

Р_l = {[(a₁, ..., a_n)] | ∑sgn_p a_i ≡ 0 mod l},

где l пробегает множество простых чисел, а sgn_p a_i означает знак элемента а_i при упорядочении р.

Если k - кольцо с инволюцией, то конструкция, аналогичная конструкции В. к., приводит к понятию группы Витта кольца с инволюцией.

С более широкой точки зрения кольцо (группа) Витта является одним из первых примеров K-функторов (см. Алгебраическая К-теория), которые играют важную роль в унитарной алгебраической K-теории.

Лит.: [1] Witt Е., «J. reine u. angew. Math. », 1936, Bd 176, S. 31-44; [2] Буpбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [3] Ленг С., Алгебра, пер. с англ., М., 1968; [4] Lorenz F., Quadratische Formen über Körpern, В. [u. a.], 1970; [5] O'Mearа О. Т., Introduction to quadratic forms, В.-Gott.-Hdlb., 1963; [6] Lam T. Y., The algebraic theory of quadratic forms, Massachusets, 1973; [7] Milnor J., Husemoller D., Symmetric bilinear forms, B. [u. a.], 1973.

А. В. Михалев, А. И. Немытов, В. Л. Попов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.