ВИТАЛИ ТЕОРЕМА

ВИТАЛИ ТЕОРЕМА - 1) В. т. о покрытии. Если система замкнутых множеств {F} является покрытием Витали (см. ниже) множества A ⊂ ℝⁿ, то из {F} можно выделить не более чем счетную последовательность попарно непересекающихся множеств {F_i}, i = 1, 2, 3, ..., такую, что

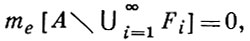
где m_e - внешняя мера Лебега в

Покрытием Витали множества A ⊂ ℝⁿ наз. система {E} подмножеств ℝⁿ такая, что для любого х ∈ А существует последовательность {Е_n} из {E}, удовлетворяющая условиям:

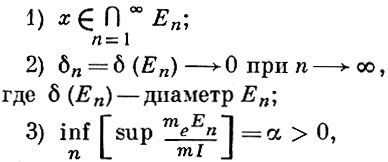
где sup берется по всем I - кубам с гранями, параллельными координатным плоскостям, содержащим Е_n, и m_e - внешняя мера Лебега в ℝⁿ (этот sup наз. параметром регулярности Е_n).

Теорема была доказана Дж. Витали [1] в случае, когда {F} состоит из кубов с гранями, параллельными координатным плоскостям. Условие, что {F} есть покрытие Витали множества А, а не покрытие в обычном смысле, существенно для справедливости В. т. Это условие не может быть опущено, даже если {F} есть система сегментов и каждому х ∈ А соответствует последовательность {F_n} из {F} с центром в х и диаметрами, стремящимися к нулю.

Лит.: [1] Vitali G., «Atti Accad. sci. Torino», 1908, v. 43, p. 75-92; [2] Сакс С., Теория интеграла, пер. с англ., М., 1949.

И. А. Виноградова.

2) В. т. о равномерной сходимости последовательности голоморфных функций: пусть последовательность {f_n(z)} голоморфных функций в области D комплексной плоскости z равномерно ограничена и сходится на множестве Е, обладающем предельной точкой в D; тогда последовательность {f_n(z)} равномерно сходится внутри D к регулярной функции, т. е. равномерно сходится на любом компактном множестве K ⊂ D. Получена Дж. Витали [1].

Компактности принцип позволяет усилить В. т., заменив в ее условии требование равномерной ограниченности в D требованием равномерной ограниченности внутри D, т. е. на любом компактном множестве K ⊂ D. Имеются также обобщения В. т. для нормальных семейств мероморфных функций, для семейств квазианалитич. функций и для семейств голоморфных функций многих комплексных переменных; в последнем случае, однако, на множество E ⊂ D ⊂ ℂⁿ необходимо наложить дополнительные ограничения, напр., что Е содержит внутренние точки в ℂⁿ (см. [3], [4]).

Лит.: [1] Vitali G., «Rend. del R. Ist. Lombardo», 2 ser., 1903, v. 36, p. 772; «Ann. mat. pura ed appl.», 3 ser., 1904, v. 10, p. 73; [2] Маркушевич А. И., Теория аналитических функций, т. 1, 2 изд., М., 1967, гл. 4; [3] Монтель П., Нормальные семейства аналитических функций, пер. с франц., М.-Л., 1936; [4] Ганнинг Р., Росси X., Аналитические функции многих комплексных переменных, пер. с англ., М., 1969.

Б. Д. Соломенцев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.