ВИРИАЛЬНОЕ РАЗЛОЖЕНИЕ

ВИРИАЛЬНОЕ РАЗЛОЖЕНИЕ, вириальный ряд - ряд в правой части уравнения состояния газа:

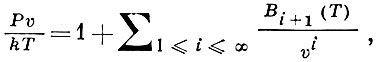
где Р - давление, Т - температура, v - удельный объем, k - постоянная Больцмана. Член ряда, содержащий к-й вириальный коэффициент B_k, характеризует отклонение газа от идеальности, связанное с взаимодействием групп из k молекул. B_k выражаются через неприводимые групповые интегралы b_k:

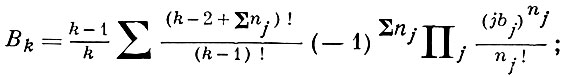
суммирование идет по всем натуральным n_j, j ὅ 2, удовлетворяющим условию

∑_2≤j≤k (j - 1) n_j = k - 1.

В частности,

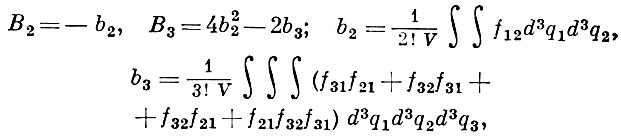
где

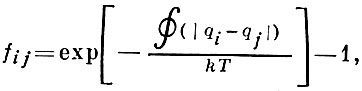
V - объем газа; интегрирование распространяется на весь объем, занятый газом. Существует правило, позволяющее с помощью f_ij записывать b_j для любого f. После упрощений оказывается:

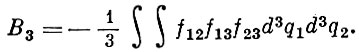
Фактически удается вычислить лишь первые вириальные коэффициенты.

Рядом по степеням v^-1 с коэффициентами, выраженными через b_j, могут быть представлены s-частичные равновесные корреляционные функции, что приводит, в частности, к простому способу получения уравнения состояния (см. [3]).

Существует квантовомеханический аналог В. р.

Лит.: [1] Майер Дж., Гепперт-Майер М., Статистическая механика, пер. с англ., М., 1952; [2] Хилл Т., Статистическая механика, пер. с англ., М., 1960; [3] Боголюбов Н. Н., Избранные труды, т. 2, Киев, 1970; [4] Уленбек Дж., Форд Дж., Лекции по статистической механике, пер. с англ., М., 1965.

И. П. Павлоцкий.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.