ВИРИАЛА ТЕОРЕМА

ВИРИАЛА ТЕОРЕМА - теорема, согласно к-рой усредненная по бесконечному интервалу времени кинетич. энергия Т̄ механич. системы равна усредненному по тому же интервалу вириалу сил, т. е.

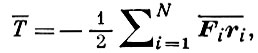
где N - число материальных точек системы, F_i - сила, действующая на i-ю точку системы, а r_i - радиус-вектор этой точки. Черта над соответствующей функцией означает усреднение этой функции по бесконечному интервалу времени.

В. т. была установлена Р. Клаузиусом (В. Clausius) в 1870 и является следствием уравнений движения механич. системы при условии, что движение системы происходит в ограниченной области пространства с ограниченными по модулю скоростями точек. В случае потенциальности сил, действующих на точки системы, соотношение (1) принимает вид

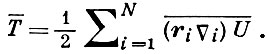
При дополнительном требовании об однородности ν-й степени потенциальной энергии относительно координат точек из (2) следует практически важное соотношение между средними значениями кинетической и потенциальной энергиями системы:

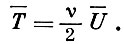
(3)

Напр., для линейного гармонического осциллятора (U ~ r², ν = 2) T̄ = Ū; а для точки, движущейся в поле тяготения Ньютона (U ~ 1/r, ν = -1), T̄ = -Ū/2.

В. т. используется в механике, статистич. механике и атомной физике (напр., для вывода уравнений состояния и определения постоянных межмолекулярных взаимодействий). В. т. в виде (2) и (3) имеет место и в квантовой механике (с соответствующими обобщениями операции усреднения и др. понятий, используемых в (2) и (3)).

Лит.: [1] Ландау Л. Д., Лифшиц Е. М., Механика, 3 изд., М., 1973; [2] Давыдов А. С., Квантовая механика, М., 1963; [3] Гиршфельдер Дж., Кертисс Ч., Берд Р., Молекулярная теория газов и жидкостей, пер. с англ., М., 1961; [4] Ольховский И. И., Курс теоретической механики для физиков, 2 изд., М., 1974.

И. И. Ольховский.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.