ВИНОГРАДОВА ОЦЕНКИ

ВИНОГРАДОВА ОЦЕНКИ - название нескольких теорем И. М. Виноградова. Наиболее известными из них являются следующие.

а) В. о. сумм характеров (см. Дирихле характер). Если χ - неглавный характер mod D, то при N > 0, М ≥ 1,

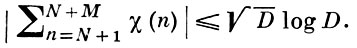
б) В. о. сумм Вейля (см. Вейля сумма). Пусть n - постоянное число с условием n ≥ 12 и пусть ν = 1/n. Пусть далее точки n-мерного пространства разбиты на два класса - точки класса 1 и точки класса 2.Точкой класса 1 наз. точка

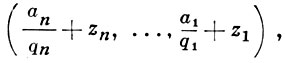
где первые слагаемые - рациональные несократимые дроби с положительными знаменателями, имеющими общим наименьшим кратным число Q, не превосходящее p^ν, а вторые слагаемые удовлетворяют условию

|z_s| ≤ p^-s+ν.

Точкой класса 2 наз. точка, не являющаяся тонкой класса 1. Тогда, если положить

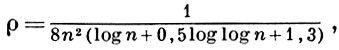
то для точек класса 2 при m ≤ Р^2ρ будет выполняться

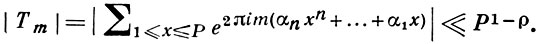
Если же положить

δ_s = z_sp^s, δ₀ = max(|δ_n|, ..., |δ₁|),

то для точек класса 1 при m ≤ Р^4ν2 будет выполняться

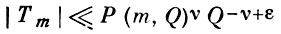
или также

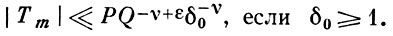
в) В. о. тригонометрических сумм с простыми числами. Пусть ε ≤ 0,001. И пусть, в обозначениях теоремы б), точки n-мерного пространства разбиты на классы следующим образом.

К классу 1а отнесены точки, удовлетворяющие условиям

Q ≤ e^uε, δ₀≤е^uε, где u = log P.

К классу 1b отнесены точки, не являющиеся тоннами класса 1а и удовлетворяющие условиям Q ≤ P^0,2ν, δ₀ ≤ P^ν.

Наконец, к классу 2 отнесены все остальные точки.

Если положить для точек класса 1a

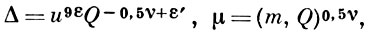
или также

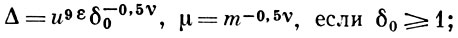
для точек класса 1b, взяв ε = 2ε', положить

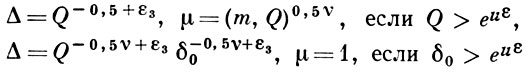
(при Q > е^uε, δ₀ > е^uε можно брать любую из указанных пар значений Δ и μ); и, наконец, для точек класса 2 положить

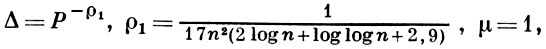
то при m ≤ Δ^-2 всегда будет выполняться

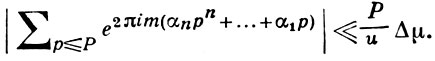
Лит.: [1] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971; [2] Хуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М., 1964.

А. А. Карацуба.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.