ВИНОГРАДОВА МЕТОД

ВИНОГРАДОВА МЕТОД - новый метод оценок тригонометрич. сумм (см. Тригонометрических сумм метод). В. м. позволяет получить очень точные оценки для широкого класса тригонометрич. сумм, в к-рых переменная суммирования пробегает значения последовательных целых чисел, последовательных простых чисел и т. д., что, в свою очередь, дает возможность решить целый ряд классич. проблем аналитич. теории чисел (распределение дробных долей широкого класса функций, распределение простых чисел в натуральном ряде, аддитивные проблемы, частными случаями к-рых являются проблемы Варинга и Гольдбаха, и др.).

Различают две части В. м.: метод оценок Вейля сумм и метод оценок тригонометрич. сумм с простыми числами. Обе части метода используют основную идею И. М. Виноградова - идею сглаживания двойной тригонометрич. суммы, к-рая состоит в следующем. Пусть дана сумма

W = ∑_u∑_v(u) ψ₂(v) e^2πiαuv,

где переменные суммирования u и v пробегают значения целых чисел (не обязательно последовательные) в количестве, соответственно, U и V, А < u < 2А, а ψ₁(u) и ψ₂(v) - произвольные комплекснозначные функции. Тогда

|W|² ≤ B ∑_A<u≤2A | ∑_vψ₂(v) e^2πiαuv,

где u пробегает последовательные целые числа интервала (А, 2А] (сглаживание),

B = ∑_v |ψ₁(u)|².

В. м. оценок сумм Вейля. Оцениваются суммы

S = ∑_1≤x≤Pe^2πif(x),

где f(x) = α_n+1xⁿ⁺¹ + ... + α₁x, причем α_n+1, ..., α₁ -действительные числа. При Y = [P^1-1/4n2] будет

S = Y^-1 ∑_1≤x≤P∑_1≤y≤Y e^2πif(x+y) + 2θY = Y^-1 ∑_1≤x≤P∑_1≤y≤Y e^2πiv + 2θY = Y^-1W + 2θY,

где = α_n+1xⁿ⁺¹ + А_n(у)хⁿ + ... + А₁(у) + А₀(y), а буквой W обозначена двойная сумма по х и у, и |θ| ≤ 1. Далее, обозначив ℬ выражение

α_n+1xⁿ⁺¹ + (A_n(y) + B_n)xⁿ + ... + (A₁(y) + B₁)x

|W| ≤ ∑_1≤y≤Y |∑_1≤x≤P e^2πiℬ| + Y_nP^1-1/4n2,

при любых В_n, ..., В₁ из области

|B_n| ≤ L_n = P^-n-1/4n2,

|B_n-1| ≤ L_n-1 = P^-n+1-1/4n2,

...,

|B₁| ≤ L₁ = P^-1-1/4n2.

При любом целом k ≥ 1:

|W|^2k ≤ 2^kY^2k-1 ∑_1≤y≤Y ∫_|Bn|≤Ln ... ∫_|B1|≤L1 |∑_1≤x≤P e^2πiℬ| dB_n ... dB₁ + 2^k (Y_nP^1-1/4n2)^2k ≤ 2^kY^2k-1 G(Y)∫¹₀ ... ∫¹₀ | ∑_1≤x≤P e^2πiℑ|^2k dγ_n ... γ₁ + 2^k (Y_nP^1-1/4n2)^2k,

где = α_n+1xⁿ⁺¹ + γ_nxⁿ + ... + γ₁x, a G(Y) - максимальное число совпадений точек с координатами

{A_n(y) + B_n}, {A_n(y) + B_n-1}, ..., {A₁(y) + B₁},

причем фигурные скобки обозначают дробную часть числа, а у меняется в пределах от 1 до Y, и

|B_n| ≤ L_n, |B_n-1| ≤ L_n-1, ..., |B₁| ≤ L₁.

При определенных арифметич. свойствах коэффициентов α_n+1, ..., α₂ многочлена f(x) для величины G(Y) можно получить оценку G(Y) ≤ Y^0,9. Кроме того, последний интеграл не превосходит числа решений системы уравнений:

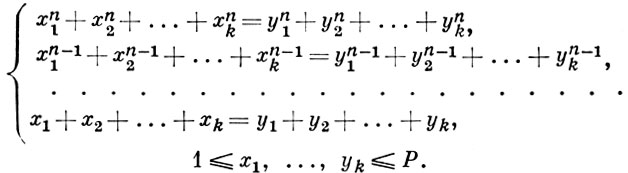
Для оценки числа решений этой системы используется Виноградова теорема о среднем, к-рая является основной в В. м. оценок сумм Вейля (см. Виноградова оценки).

В. м. оценок тригонометрических сумм с простыми числами. Оцениваются суммы

S' = ∑_p≤P e^2πif(p),

где f(p) = α_nрⁿ + ... + α₁р, а_n, ..., а₁ - действительные числа. Пусть D = П_p≤H, где H ≤ р^0,25. С помощью известного свойства функции Мебиуса S' сводится к небольшому числу сумм (это число не превосходит ln P/ln H) вида

W_S = ∑_d1\D ... ∑_ds\D∑_m1>0 ... ∑_ms>0 μ(d₁) ... μ(d_s) × e^{2πif(m₁...m_sd₁...d_s)},

где m₁...m_sd₁...d_s ≤ Р. В кратной сумме W_s переменные m₁...m_s пробегают сплошные интервалы суммирования. Те суммы W_s, в к-рых интервал суммирования хотя бы по одной переменной m длинный, оцениваются с помощью В. м. оценок сумм Вейля. В противном случае длинным будет интервал суммирования по одной из переменных суммирования d, d\D. Тогда применяется следующая лемма И. М. Виноградова, к-рая вместе с идеей сглаживания двойных сумм является основной в В. м. оценок тригонометрич. сумм с простыми числами.

Лемма. Пусть 0 ≤ σ ≤ 1/3 и D - произведение всех простых чисел, не превосходящих х^σ, тогда все делители d числа D, не превосходящие х, можно распределить среди менее чем х^ε совокупностей со следующими свойствами:

а) числа d, принадлежащие одной совокупности, обладают одним и тем же числом β простых сомножителей и, следовательно, одним и тем же значением μ(d) = (-1)^β;

б) одна из совокупностей, к-рая наз. простейшей, состоит из одного числа d = 1. Для каждой из остальных совокупностей имеется свое φ такое, что все числа этой совокупности удовлетворяют условию

φ < d ≤ φ^1+ε₁, ε₁ = ε₁(ε);

в) для всякой совокупности, отличной от простейшей, при любом U с условием 0 ≤ U ≤ φ существуют две совокупности чисел d: числа d' и d'' с отвечающими им числами φ' и φ'', к-рые удовлетворяют условиям

U < φ' ≤ Ux^σ, φ'φ'' = φ,

такие, что при нек-ром натуральном В все числа выбранной совокупности, каждое В раз получим, если из всех произведений d'd'' выберем лишь удовлетворяющие условию (d', d'') = 1.

Применяя пункт в) этой леммы с надлежащим значением U, получают

W_s = ∑_u∑_v ψ₁(u) ψ₂(v) e^2πif(uv),

где переменные u и v пробегают длинные интервалы суммирования. Из этой леммы может быть выведена оценка И. М. Виноградова тригонометрия, суммы с простыми числами (см. Виноградова оценки).

Если F(х) в определенном смысле хорошо приближается многочленом, то В. м. позволяет оценивать суммы вида

S = ∑_1≤x≤Pe^2πiF(x), S' = ∑_p≤P e^2πiF()p

(см. [2], [4]). Кроме того, В. м. позволяет оценивать суммы вида

∑_p≤P χ(p + a), ∑_1≤n≤N μ(n) χ(n + a)

и т. п. Это дает возможность решать проблемы распределения степенных вычетов, первообразных корней и др. в последовательностях вида р + а, где а > 0 - фиксированное целое число, а р принимает значения последовательных простых чисел (см. [3], [5]). О применениях В. м. в аналитич. теории чисел см. [1], [2], [4], [5], [6].

Лит.: [1] Виноградов И. М., Метод тригонометрических сумм в теории чисел, М., 1971; [2] его же, Избранные труды, М., 1952; [3] его же, «Изв. АН СССР. Сер. матем.», т. 30, № 3, 1966, с. 481-96; [4] Карацуба А. А., «Труды Матем. ин-та АН СССР», 1971, т. 112, с. 241 - 55; 1973, т. 122, с. 257-61; [5] Хуа Ло-ген, Метод тригонометрических сумм и его применения в теории чисел, пер. с нем., М 1964; [6] Чандрасекхаран К., Арифметические функции, пер. с англ., М., 1974.

А. А. Карацуба.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.