ВИНОГРАДОВА ГИПОТЕЗЫ

ВИНОГРАДОВА ГИПОТЕЗЫ - ряд гипотез относительно центральных проблем аналитической теории чисел, высказанных в разное время И. М. Виноградовым [1]-[3].

Гипотезы о распределении степенных вычетов и невычетов. Одной из самых старых и знаменитых из них является гипотеза о том, что расстояние между соседними квадратичными невычетами mod р есть величина порядка р^ε.

Гипотезы об оценках тригонометрических сумм. Одной из них является гипотеза о том, что

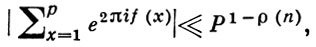
где

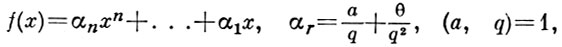
|θ| ≤ 1, P^0,25 < g < P^r-0,25, r - одно из чисел 2, ..., n и ρ(n) имеет порядок n^-1-ε.

Гипотезы о количестве решений диофантовых уравнений. Одной из них является гипотеза о том, что число решений системы уравнений

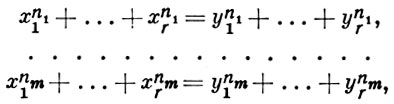
1 ≤ х_i, y_i < Р, i = 1, ..., r, 1 ≤ n₁ < ... < n_m = n, при постоянном n будет величиною порядка

p^2r-k, k = n₁ + ... + n_m,

при всех r ≥ r₀, где r₀ имеет порядок k^1+ε.

Гипотезы о количестве целых точек в областях на плоскости и пространстве. Одной из них является гипотеза о том, что число целых точек в шаре х² + у² + z² ≤ R² выражается формулой

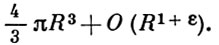
Лит.: [1] Виноградов И. М., Некоторые проблемы аналитической теории чисел, в кн.: Тр. третьего Всесоюзного математического съезда, т. 3, М., 1958, с. 3-13; [2] его же, Метод тригонометрических сумм в теории чисел, М., 1971; [3] его же, Избранные труды, М., 1952.

А. А. Карацуба.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.