ВИНЕРОВСКИЙ ПРОЦЕСС

ВИНЕРОВСКИЙ ПРОЦЕСС - однородный гауссовский процесс X(t) с независимыми приращениями. В. п. служит одной из математич. моделей для процесса броуновского движения. Простым преобразованием В. п. может быть превращен в «стандартный» В. п. X(t), t ≥ 0, для к-рого

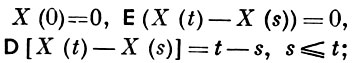
при таких средних значениях и дисперсиях приращений это единственный непрерывный с вероятностью 1 процесс с независимыми приращениями. Ниже под В. п. будет пониматься именно этот процесс.

В. п. X(t), 0 ≤ t ≤ 1, определяется также как гауссовский случайный процесс с нулевым математич. ожиданием и корреляционной функцией

В(s, t) = min (s, t).

В. п. X = X(t), t ὅ 0, может быть определен как однородный марковский процесс с переходной функцией

Р(t, х, Г) = ∫_Г p(t, х, у) dy,

где переходная плотность p(t, x, y) есть фундаментальное решение параболического дифференциального уравнения

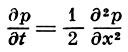
и описывается формулой

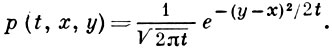
Переходная функция Р(t, х, Г) инвариантна относительно преобразований сдвига в фазовом пространстве:

P(t, x + y, Г) = P(t, z, Г - у),

где Г - у обозначает множество {z : z + у ∈ Г}.

В. п. является непрерывным аналогом случайного блуждания частицы, к-рая в дискретные моменты времени t = kΔt (кратные Δt) в результате случайного воздействия каждый раз независимо от предшествующих обстоятельств смещается на величину ΔX(t) (ЕΔХ(t) = 0, DΔX(t) = Δt); точнее, если при Δt = 1/n

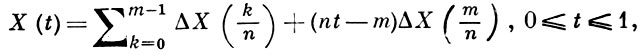
- случайная траектория движения такой частицы на отрезке [0, 1] (здесь Δt = 1/n, m = [nt] - целая часть nt, X(t) = ntΔX(0) при 0 ≤ t < 1/n), а Р_n - соответствующее распределение вероятностей в пространстве непрерывных функций x = x(t), 0 ≤ t ≤ 1, то распределение вероятностей Р траектории В. п. X(t), 0 ≤ t ≤ 1, является предельным (в смысле слабой сходимости) для распределений Р_n при n → ∞: P_n ⇒ Р.

Как функция со значениями в гильбертовом пространстве L²(Ω) всех случайных величин X, ЕХ² < ∞, в к-ром скалярное произведение определено формулой

〈X₁, Х₂〉 = ЕХ₁Х₂,

В. п. Х = Х(t), 0 ≤ t ≤ 1, допускает следующее каноническое представление:

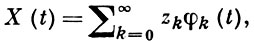
где z_k - независимые гауссовские величины:

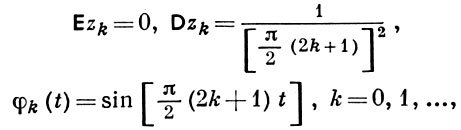
- собственные функции оператора В, определенного формулой:

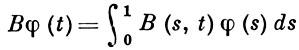
в гильбертовом пространстве L²[0, 1] всех интегрируемых с квадратом (относительно лебеговской меры) функций Δ = Δ(t) на отрезке [0, 1].

Для почти всех траекторий В. п. имеют место следующие соотношения:

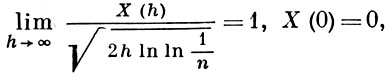
- закон повторного логарифма;

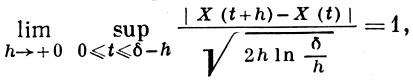
что характеризует модуль непрерывности на отрезке [0, h];

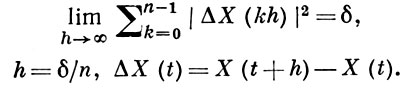
В применении к В. п. вида Х₁(t) = tX(1/t), 0 ≤ t < ∞, закон повторного логарифма записывается в форме:

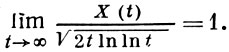
Характер смещения броуновской частицы за конечное время t может быть описан с помощью распределения вероятностей максимума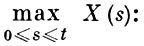

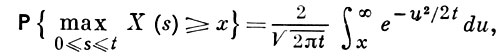
0 ≤ x < ∞, t фиксировано, 0 ≤ t < ∞, а также с помощью распределения времени т первого достижения броуновской частицей фиксированной точки х > 0:

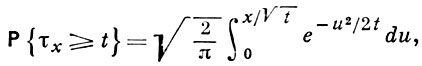
0 ≤ t < ∞, х фиксировано, 0 ≤ х < ∞ (закономерности В. п. остаются без изменения при преобразовании фазового пространства х → -х). Совместное распределение точки максимума τ, 0 ≤ τ ≤ t, и самого максимума 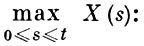имеет плотность вероятности

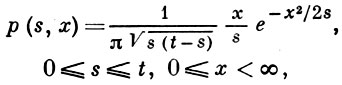
а отдельно взятая точка τ (с вероятностью 1 имеется лишь один максимум на отрезке 0 ≤ s ≤ 0 распределена по арксинуса закону:

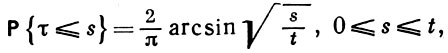
с плотностью вероятности

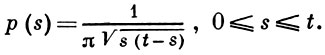
Из приведенных выше формул легко выводятся следующие характерные свойства В. п. Броуновская траектория является нигде не дифференцируемой, причем при выходе из к.-л. точки х эта траектория за сколь угодно малое время δ с вероятностью 1 бесконечно много раз пересекает «уровень» х (возвращаясь в исходную точку); с течением времени t броуновская траектория обходит все точки х, точнее τ_x < ∞, с вероятностью 1 (при этом вероятное значение τ_x для больших х имеет порядок х²); рассматриваемая на фиксированном отрезке [0, t], эта траектория имеет тенденцию достигать экстремальных значений вблизи концевых точек s = 0 и s = t.

Для В. п. как марковского однородного процесса существует инвариантная мера Q(dx):

Q(A) = ∫ Q(dx) P(t, x, A),

к-рая в силу упомянутого выше свойства инвариантности переходной функции Р(t, х, А) совпадает с лебеговской мерой на прямой: Q(dx) = dx. Время Т(А), проведенное броуновской частицей в множестве А за промежуток от 0 до Т, таково, что с вероятностью 1

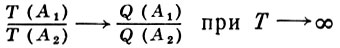
для любых ограниченных борелевских множеств А₁ и А₂.

Аналогом В. п. X = X(t) для векторного параметра t = (t₁, ..., t_n) являются случайные поля, введенные П. Леви (P. Lévy, см. [31).

Лит.: [1] Ито К., Маккин Г., Диффузионные процессы и их траектории, пер. с англ., М., 1968; [2] Прохоров Ю. В., Розанов Ю. А., Теория вероятностей, 2 изд., М., 1973; [3] Lévy P., Prossesus stochastuiues et mouvément brownien, 2 éd., P., 1965; [4] Павлов В. П., Броуновское движение, в кн.: БСЭ, 3 изд., т. 4.

Ю. А. Розанов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.