ВИНЕРА-ХОПФА УРАВНЕНИЕ

ВИНЕРА-ХОПФА УРАВНЕНИЕ - интегральное уравнение на полупрямой с ядром, зависящим от разности аргументов:

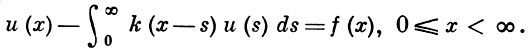
(1)

Уравнения такого типа часто возникают в задачах математич. физики, напр. в теории переноса излучения (проблема Милна), в теории дифракции (дифракция на полуплоскости, задача береговой рефракции).

Впервые исследования уравнения (1) были проведены в работах [1] и [2], где был развит метод факторизации (см. Винера-Хопфа метод). Именно идея факторизации явилась решающей для построения теории интегральных уравнений вида (1). В.-X. у. в предположении четности и экспоненциального убывания ядра k(х) рассматривались в [3].

Формальная схема решения В.-X. у. состоит в следующем. Пусть

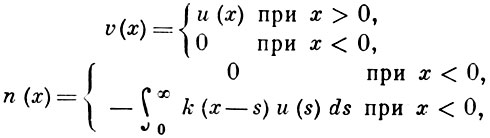
тогда уравнение (1) можно записать на всей бесконечной прямой:

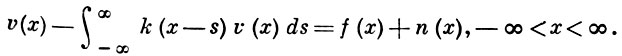
(2)

Если выполнены условия, при к-рых существует преобразование Фурье всех функций, входящих в уравнение (2):

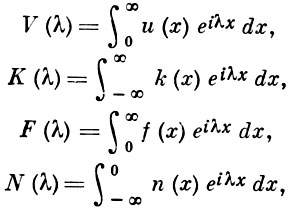
то с помощью преобразования Фурье уравнение (2) сводится к функциональному уравнению

[1 - K(λ)] V(λ) = F(λ) + N(λ), (3)

где V(λ) и N(λ) - неизвестные функции. Метод Винера-Хопфа позволяет решить уравнение (3) для определенного класса функций. При этом обязательно должно выполняться условие: 1 - К(λ) ≠ 0. Для несимметричного ядра в теории уравнения (1) особую роль играет индекс уравнения:

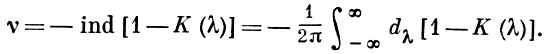
(4)

Если K(x) ∈ L₁(-∞, ∞) и 1 - K(λ) ≠ 0, то: при ν = 0 неоднородное уравнение (1) имеет единственное решение; при ν > 0 однородное уравнение (1) имеет ν линейно независимых решений; при ν < 0 неоднородное уравнение (1) либо не имеет решения, либо имеет единственное решение при условии:

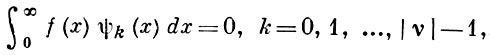
где ψ_k(х) - линейно независимые решения транспонированного однородного уравнения (1)

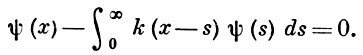
Лит.: [1] Wiener N., Hopf E., Über eine Klasse singulärer Integralgleichungen, «Sitz. Akad. Wiss.», В., 1931; [2] Hopf E., Mathematical problems of radiative equilibrium, Camb., 1934; [3] Фок В. А., «Матем. сб.», 1944, т. 14, № 1-2, с. 3-50; [4] Нобл Б., Применение метода Винера-Хопфа для решения дифференциальных уравнений в частных производных, пер. с англ., М., 1962.

В. И. Дмитриев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.