ВИНЕРА-ХОПФА МЕТОД

ВИНЕРА-ХОПФА МЕТОД - метод решения функционального уравнения вида:

А(λ)Ф₊(λ) + B(λ)Ф_-(λ) + C(λ) = 0, (1)

где А(λ), В(λ), С(λ) - заданные функции комплексного переменного λ, аналитические в полосе τ_- < Im λ < τ₊, причем А(λ) и В(λ) отличны от нуля в этой полосе; функции Ф₊(λ) и Ф_-(λ) - неизвестные функции комплексного переменного λ, стремящиеся к нулю при |λ| → ∞ и подлежащие определению, причем Ф₊(λ) аналитична при Im λ > τ_-, а Ф_-(λ) аналитична при Im λ < т₊. Уравнение (1) выполняется в общей полосе аналитичности τ_- < Im λ < τ₊.

Основой В.-X. м. являются следующие две теоремы. 1) Функция F(λ), аналитическая в полосе τ_- < Im λ < τ₊ и равномерно стремящаяся к нулю при |λ| → ∞, представима в этой полосе в виде суммы:

F(λ) = F₊(λ) + F_-(λ),

где F₊(λ) аналитична в полуплоскости Im λ > τ_-, a F_-(λ) аналитична в полуплоскости Im λ < τ₊.

2) Функция F(λ), аналитическая и отличная от нуля в полосе τ_- < Im λ < τ₊ и равномерно стремящаяся в этой полосе к единице при |λ| → ∞, представима в данной полосе в виде произведения:

F(λ) = F₊(λ) ⋅ F_-(λ), (2)

где F₊(λ) и F_-(λ) аналитичны и отличны от нуля, соответственно, в полуплоскостях Im λ > τ_- и Im λ < τ₊. Представление (2) часто наз. факторизацией функции F(λ).

Основная идея В.-X. м. заключается в возможности факторизации функции L(λ) = А(λ)/B(λ), т. е. в возможности представления

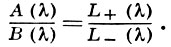
(3)

Используя (3), уравнение (1) можно переписать в виде:

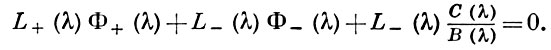
Поскольку L_-(λ)С(λ)/В(λ) аналитична в полосе, то

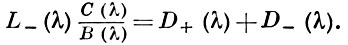
Используя (4), получают окончательно уравнение (1) в виде:

L₊Ф₊ + D₊ = - D_- - L_-Ф_-. (5)

Левая часть выражения (5) представляет собой функцию, аналитическую в Im λ > τ_-, а правая - функцию, аналитическую в Im λ < τ₊. Так как они имеют общую полосу аналитичности, где выполняется условие (5), то существует единственная целая функция F(λ), совпадающая, соответственно, с левой и правой частями (5) в областях их аналитичности. Отсюда

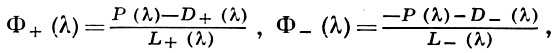
т. е. решение уравнения (1) определено с точностью до целой функции. Если степень роста функций L(λ) и D(λ) ограничена на бесконечности, то Р(λ) будет многочленом. Тогда искомые функции определяются с точностью до постоянных, к-рые вычисляются из дополнительных условий.

В. -X. м. был разработан в [1] для решения интегральных уравнений специального вида (см. Винера-Хопфа уравнение). В дальнейшем он нашел широкое применение в различных задачах математич. физики (см. также [2]).

Лит.: [1] Wiener N., Hopf Е., Über eine Klasse singularer Integralgleichungen, «Sitz. Akad. Wiss.», В., 1931; [2] Нобл Б., Применение метода Винера-Хопфа для решения дифференциальных уравнений в частных производных, пер. с англ., М., 1962.

В. И. Дмитриев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.