ВИНЕРА МЕРА

ВИНЕРА МЕРА, винеровская мера, - вероятностная мера μ_W, определенная на пространстве С[0, 1] непрерывных числовых функций x(t), заданных на отрезке [0, 1], следующим образом. Пусть 0 < t₁ < ... < t_n ≤ 1 - произвольный набор точек из [0, 1], А₁, ..., А_n - борелевские множества на прямой. Пусть С(t₁, ..., t_n, А₁, ..., А_n) обозначает множество функций x(t) из С[0, 1], для к-рых x(t_k) ∈ A_k, k = 1, ..., n.

Тогда

μ_W(C(t₁, ..., t_n; А₁, ..., А_n)) = ∫_А1 p(t₁, x₁) dx₁ ∫_А2 p(t₂ - t₁, x₂ - x₁) dx₂ ... ∫_Аn p(t_n - t_n-1, x_n - x_n-1) dx_n, (*)

где

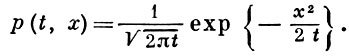
С помощью теоремы о продолжении меры можно, исходя из равенства (*), определить значение меры μ_W на всех борелевских множествах пространства С[0, 1].

А. В. Скороход.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.