ВЗАИМНОСТИ ЗАКОНЫ

ВЗАИМНОСТИ ЗАКОНЫ - ряд утверждений, касающихся связи между символами степенных или норменных вычетов.

Простейшим проявлением В. з. является следующий факт, известный еще П. Ферма (P. Fermat). Простыми делителями чисел х² + 1 могут быть лишь число 2 и простые числа, лежащие в арифметич. прогрессии 1 + 4k. Другими словами, сравнение

х² + 1 ≡ 0 (mod р)

по простому модулю р >2 разрешимо в томи только в том случае, когда р ≡ 1 (mod 4). С помощью символа квадратичного вычета (a/p) (Лежандра символа) последнее утверждение может быть выражено следующим образом:

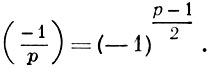
В более общем случае вопрос о разрешимости сравнения

х² ≡ а (mod р) (*)

решается с помощью Гаусса закона взаимности:

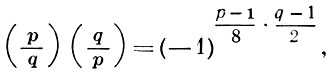
где р и q - различные нечетные простые числа, а также двух дополнений к этому закону

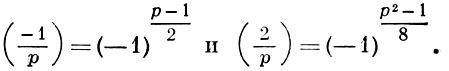
Из этих соотношений для символов Лежандра следует, что простые числа р, для к-рых сравнение (*) при фиксированном а разрешимо, укладываются ровно в половину приведенных классов вычетов по модулю 4|а|.

К. Гаусс (С. Gauss) справедливо придавал большое значение указанному В. з. и дал несколько его доказательств, основанных на совершенно различных идеях [1]. Из закона взаимности Гаусса и его дальнейшего обобщения - В. з. для Якоби символа - следует, в частности, что тип разложения простого числа р в квадратичном расширении ℚ(√d) поля рациональных чисел ℚ определяется вычетом р по модулю 4|d|.

Закон взаимности Гаусса обобщается на сравнения вида

хⁿ = a (mod р), n > 2.

Однако при этом происходит переход от арифметики целых рациональных чисел к арифметике целых чисел расширения К конечной степени m поля рациональных чисел. Кроме того, для обобщения В. з. на вычеты n-й степени нужно предполагать, что рассматриваемое расширение содержит примитивный корень ζ степени n из 1. При таком предположении для простых дивизоров ℬ поля К, не делящих n, имеет место сравнение

N_ℬ ≡ 1 (mod n),

где N_ℬ - норма дивизора ℬ, равная числу классов вычетов максимального порядка этого поля по модулю ℬ. Аналог символа Лежандра определяется при помощи сравнения

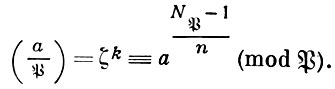
Символ степенного вычета (a/b) для пары целых чисел а и b, аналогичный символу Якоби, определяется по формуле

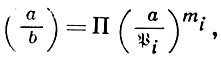
если (b) = Пℬ_i^m_i - разложение главного дивизора (b) на простые сомножители и если b взаимно просто с аn.

В. з. для n = 4 в поле ℚ(i) был установлен К. Гауссом [2], для n = 3 в поле ℚ(е^2πi/3) - Г. Эйзенштейном [3]. Общий В. з. для символа степенного вычета в поле ℚ(е^2πi/n) простой степени n был установлен Э. Куммером [4]. Формула Куммера для регулярного простого числа n имеет вид

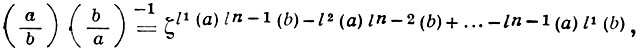
где а, b - целые числа поля ℚ(е^2πi/n),

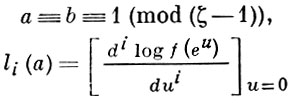
и f(t) - многочлен степени n-1 такой, что

а = f(ζ), f(1) = 1.

Следующий этап в изучении общих В. з. связан с работами Д. Гильберта [5], [6], выяснившего их локальный аспект. Д. Гильберт для нек-рых случаев установил В. з. в виде формулы произведения для его символа норменного вычета

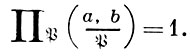
Он подметил также аналогию этой формулы с теоремой о вычетах алгебраич. функций - простые точки ℬ с символом норменного вычета ≠1 соответствуют точкам ветвления на римановой поверхности.

Дальнейший прогресс в изучении В. з. связан с именами Ф. Фуртвенглера [7], Т. Такаги [8], Э. Артина [9], X. Хассе [10]. Наиболее общая форма В. з. была получена И. Р. Шафаревичем [11].

Как и закон взаимности Гаусса, общие В. з. тесно связаны с задачей изучения законов разложения простых дивизоров ℬ заданного поля алгебраич. чисел k в его алгебраич. расширениях K/k с абелевой Галуа группой. В частности, теория полей классов, решающая эту задачу, может быть обоснована (см. [12]), исходя из закона взаимности Шафаревича.

Лит.: [1] Gauss С. F., Werke, Bd 1 - Disquisitiones arithmeticae, Gütt., 1870; [2] его же, Theoria residuorum biquadraticorum. Commentatio prima et secunda, в кн.: Werke, Bd 2, Gütt., 1863, S. 65, 93; [3] Eisenstein G., «J. Math.», 1844, Bd 27; [4] Kummer E., «Веr. K. Akad. Wiss. Berlin», 1850; [5] Hilbert D., «Jahresber. Dtsch. Math.-Ver.», 1897, Bd 4, S. 175-546; [6] его же, там же, 1899, Bd 6, № 1, S. 88-94; [7] Furtwängler Ph., «Math. Ann.», 1909, Bd 67, S. 1-31; 1912, Bd 72, S. 346-86; 1913, Bd 74, S. 413-29; [8] Takagi Т., «J. Colloid Science», 1920, v. 41, t. 9; [9] Artin E., «Abh. Math. Semin. Hamburg Univ.», 1928, Bd 5; [10] Hasse H., «Math. Ann.», 1933. Bd 107, № 5, S. 731-60; [11] Шафapeвич И. P., «Успехи матем. наук», 1948, т. 3, в. 3 (25), с. 165; [12] Лапин А. И., «Изв. АН СССР. Сер. матем.», 1954, т. 18, № 4, с. 335-78; [13] Алгебраическая теория чисел, пер. с англ., М., 1969; [14] Фаддеев Д. К., в кн.: Проблемы Гильберта, М., 1969 С. 131-40.

С. А. Степанов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.