ВЕЩЕСТВЕННОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО

ВЕЩЕСТВЕННОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО - аналитическое пространство над полем ℝ действительных чисел. В отличие от комплексных аналитич. пространств, структурные пучки В. а. п. могут не быть когерентными пучками. В. а. п. наз. когерентным, если его структурный пучок когерентен. Все вещественные аналитич. многообразия (т. е. гладкие В. а. п.) являются когерентными В. а. п.

Пусть V_a - росток в точке а вещественного аналитич. подмножества пространства ∨ⁿ. Тогда определен росток в точке а комплексного аналитич. подмножества Ṽ_a пространства ℂⁿ. обладающий следующими эквивалентными свойствами: а) Ṽ_a есть пересечение всех ростков комплексных аналитич. множеств, содержащих V_a; б) если 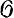_Va - аналитич. алгебра ростка V_a, то 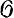_Va ⊗ ℂ есть аналитич. алгебра ростка Ṽ_a. Росток Ṽ_a наз. комплекс и фикацией ростка V_a, а V_a -вещественной частью ростка Ṽ_a. Аналогично для всякого когерентного В. а. п. X можно построить комплексификацию X̃, являющуюся комплексным аналитич. пространством. При этом X будет обладать в X̃ фундаментальной системой окрестностей, являющихся Штейна пространствами.

Теория когерентных В. а. п. аналогична теории комплексных пространств Штейна. Глобальные сечения всякого когерентного аналитического пучка модулей F на когерентном В. а. п. X порождают модули ростков его сечений в любой точке пространства X, и все группы Н^q(Х, F) равны нулю при q ≥ 1.

Для всякого конечномерного когерентного В. а. п. (x, 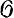_x) существует морфизм

f = (f₀, f₁):(X, 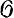_X) → (ℝ 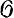_ℝⁿ)

такой, что f₀ - собственное взаимно однозначное отображение пространства X на когерентное подпространство в ℝⁿ, причем f - вложение в гладких точках пространства X. В частности, всякое (хаусдорфово и счетное в бесконечности) вещественное аналитич. многообразие изоморфно вещественному аналитич. подмногообразию в ℝⁿ. Для приведенного когерентного В. а. п. X множество классов изоморфных вещественно аналитич. главных расслоений со структурной вещественной группой Ли G, допускающей комплексификацию, и базой X находится во взаимно однозначном соответствии с множеством классов изоморфных топологич. главных расслоений с той же структурной группой G.

Лит.: [1] Espaces analytiques, Вuc, 1971, р. 149-57.

Д. А. Пономарев.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.