ВЕТВЯЩИЙСЯ ПРОЦЕСС С КОНЕЧНЫМ ЧИСЛОМ ТИПОВ ЧАСТИЦ

ВЕТВЯЩИЙСЯ ПРОЦЕСС С КОНЕЧНЫМ ЧИСЛОМ ТИПОВ ЧАСТИЦ - модель ветвящегося процесса, являющаяся частным случаем марковского процесса со счетным множеством состояний. Состояние ветвящегося процесса описывается случайным вектором

μ(t) = (μ₁, ..., μ_n(t)),

k-я компонента к-рого μ_k(t) показывает, что в момент t имеется μ_k(t) частиц типа T_k. Основное свойство, выделяющее ветвящиеся процессы из марковских, состоит в том, что частицы, существующие в момент t₁, в любой следующий момент t₁ + t, t > 0, дают потомство независимо друг от друга. При этом производящие функции

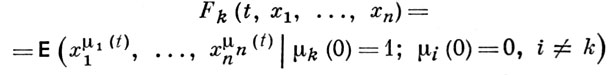
удовлетворяют системе уравнений

F_k(t + τ, х₁, ..., х_n) = F_k(t, F₁(τ, x₁, ..., х_n), ..., F_n(τ, х₁, ..., х_n)) (*)

и начальным условиям

F_k(0, х₁, ..., х_n) = х_k, k = 1, 2, ..., n.

Уравнениям (*) удовлетворяют процессы с дискретным и с непрерывным временем.

В случае дискретного времени матрица математич. ожиданий

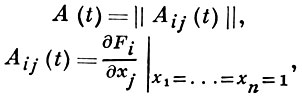
является t-й степенью матрицы А = А(1): A (t) = A^t. Если матрица А неразложима и непериодична, то она имеет простое положительное характеристич. число λ, к-рое больше модулей остальных характеристич. чисел. В этом случае при t → ∞

A_ij(t) = u_iv_jλ^t + o(λ^t),

где (u₁, ..., u_n), (v₁, ..., v_n) - правый и левый собственные векторы матрицы А, соответствующие λ. Ветвящиеся процессы с неразложимой матрицей А наз. докритическими, если λ < 1, надкритическими, если λ > 1, и критическими, если λ = 1 и хотя бы одна из функций F_k(1, x₁, ..., x_n) нелинейна. Для процессов с непрерывным временем понятие критичности вводится аналогично.

Асимптотич. свойства ветвящегося процесса существенно зависят от критичности. Докритич. и критич. процессы вырождаются с вероятностью 1. Асимптотические при t → ∞ формулы для вероятности

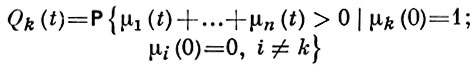
и теоремы о предельных распределениях числа частиц [2] аналогичны соответствующим результатам для процессов с одним типом частиц (см. Ветвящийся процесс). Изучены асимптотич. свойства процессов, близких к критическим (t → ∞, λ → 1) (см. [3]). Изучаются также процессы с разложимой матрицей математич. ожиданий (см. [4]).

Лит.: [1] Колмогоров А. Н., Дмитриевы. А., «Докл. АН СССР», 1947, т. 56, № 1, с. 7-10; [2] Севастьянов Б. А., Ветвящиеся процессы, М., 1971; [3] Чистяков В. П., «Теории вероят. и ее примен.», 1972, т. 17, № 4, с. 669-78; [4] Оgura J., «J. Math. Kyoto Univ.», ser. A, 1975, v. 15, № 2, p. 251-302.

В. П. Чистяков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.