ВЕТВЯЩИЙСЯ ПРОЦЕСС С ЗАВИСИМОСТЬЮ ОТ ВОЗРАСТА

ВЕТВЯЩИЙСЯ ПРОЦЕСС С ЗАВИСИМОСТЬЮ ОТ ВОЗРАСТА - модель ветвящегося процесса, в к-ром время жизни частицы является произвольной неотрицательной случайной величиной, а число потомков частицы зависит от ее возраста в момент превращения. В модели с однотипными частицами каждая частица имеет случайную продолжительность жизни τ с функцией распределения

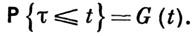
В конце жизни частица превращается в k частиц нулевого возраста с вероятностью р_k(u), если превращение произошло, когда частица достигла возраста u. Пусть μ(t) - число частиц в момент времени t. Производящая функция F(t, х) распределения вероятностей μ(t) для процесса, начавшегося с одной частицы нулевого возраста, удовлетворяет уравнению

(*)

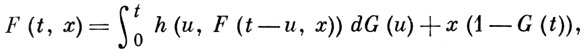
где

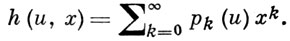
Положим

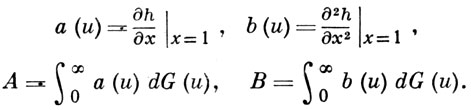
В. п. с з. от в. наз. докритическим, критическим или надкритическим, если соответственно А < 1, А = 1 и В > 0, А > 1. Поведение процесса при t → ∞ существенно зависит от критичности процесса. Докритич. и критич. процессы вырождаются с вероятностью 1, т. е.

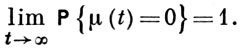
Для рассматриваемых процессов получены [1] асимптотич. формулы моментов μ(t), необходимые и достаточные условия вырождения, условия существования и единственности решения уравнения (*), асимптотич. формулы при t → ∞ для

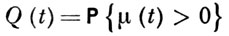
и найдены предельные распределения. В критич. случае при t → ∞:

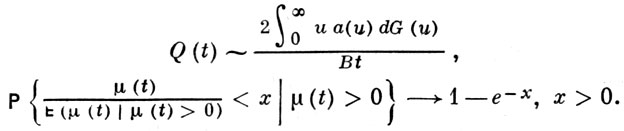
В случае, когда h(u, х) не зависит от u, В. п. с з. от в. - Беллмана-Харриса процесс. Имеются обобщения описанной модели на процессы с несколькими типами частиц, а также на процессы с предположением, что частица может в течение жизни порождать новые частицы несколько раз (см. [2], [3]).

Лит.: [1] Севастьянов Б. А., Ветвящиеся процессы, М 1971; [2] его же, «Теория вероят. и ее примен.», 1964, т. 9, № 4, с. 577-94; [3] Mode С. J., Multitype Branching Processes, N. Y., 1971.

В. П. Чистяков.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.