ВЕТВЯЩИЙСЯ ПРОЦЕСС С ДИФФУЗИЕЙ

ВЕТВЯЩИЙСЯ ПРОЦЕСС С ДИФФУЗИЕЙ - модель ветвящегося процесса, в к-ром размножающиеся частицы диффундируют в к.-л. области G. Пусть область G r-мерна, ее граница ∂G - поглощающая, и в самой области частицы независимо друг от друга совершают броуновское движение. Каждая частица в области G за время Δt → 0 независимо от других частиц с вероятностью p_nΔt + o(Δt), n ≠ 1, превращается в n частиц, к-рые независимо друг от друга начинают свою эволюцию из точки их рождения. Пусть

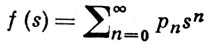
- производящая функция {p_n}, p₁ = -∑_n≠1p_n, μ_xt(A) - число частиц в множестве А ⊆ G в момент t, если в начальный момент была одна частица в точке x ∈ G. Производящий функционал

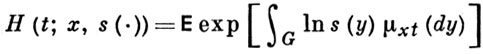
удовлетворяет квазилинейному параболич. уравнению

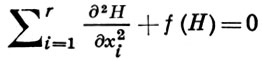
с начальным условием

H(0, х, s(⋅)) = s(x)

и граничным условием

H(t, х, s(⋅))|_x→∂G = 0.

Обозначим 0 < λ₁ < λ₂ ≤ λ₃ ≤... собственные значения, φ₁(x) > 0 - соответствующую λ₁ собственную функцию задачи

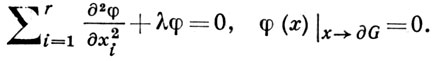
При t → ∞ имеет место асимптотика

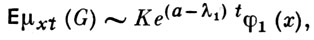
в соответствии с к-рой процесс наз. докритическим при a < λ₁ критическим при а = λ₁ и надкритическим при а > λ₁. При а ≤ λ₁ В. п. с д. вырождается с вероятностью 1, а при а > λ₁ с положительной вероятностью μ_xt(G) → ∞ при t → ∞. В зависимости от критичности В. п. с д. имеют место предельные теоремы, аналогичные теоремам для ветвящихся процессов без диффузии.

Лит.: [1] Севастьянов Б. А., Ветвящиеся процессы, М., 1971.

Б. А. Севастьянов.

Источники:

1. Математическая Энциклопедия. Т. 1 (А - Г). Ред. коллегия: И. М. Виноградов (глав ред) [и др.] - М., «Советская Энциклопедия», 1977, 1152 стб. с илл.